\(\dfrac{\sqrt[3]{4}+\sqrt[3]{2}+2}{\sqrt[3]{4}+\sqrt[3]{2}+1}\)​

\(=\dfrac{\sqrt[3]{4}+\sqrt[3]{2}+\sqrt[3]{8}}{\sqrt[3]{4}+\sqrt[3]{2}+1}=\dfrac{\sqrt[3]{2}\left(\sqrt[3]{2}+1+\sqrt[3]{4}\right)}{\sqrt[3]{4}+\sqrt[3]{2}+\sqrt[3]{1}}=\sqrt[3]{2}\)

Vì mạch thứ 2 có 5% nuclêôtit loại G và bằng nuclêôtit loại X, ta có tỷ lệ như sau:

• Nuclêôtit loại G: 5%
• Nuclêôtit loại X: 5%

Do đó, tỷ lệ của các loại nuclêôtit còn lại là:

• Nuclêôtit loại A: (100% - 5% - 5%) / 2 = 45%
• Nuclêôtit loại T: (100% - 5% - 5%) / 2 = 45%

Tổng số nuclêôtit của gen sẽ bằng tổng số nuclêôtit của mạch thứ 2, nhân với 2 (vì mỗi mạch gồm 2 chuỗi nuclêôtit):
Tổng số nuclêôtit của gen = 2 * (5% + 5% + 45% + 45%) = 2 * 100% = 200

Vậy, tổng số nuclêôtit của gen là 200.

b) Để tính khối lượng và chiều dài của gen, ta cần biết khối lượng và chiều dài trung bình của mỗi nuclêôtit.

Giả sử khối lượng trung bình của mỗi nuclêôtit là m và chiều dài trung bình của mỗi nuclêôtit là l.

Khối lượng của gen sẽ bằng tổng khối lượng của tất cả các nuclêôtit trong gen:
Khối lượng của gen = Tổng số nuclêôtit của gen * khối lượng trung bình của mỗi nuclêôtit = 200 * m

Chiều dài của gen sẽ bằng tổng chiều dài của tất cả các nuclêôtit trong gen:
Chiều dài của gen = Tổng số nuclêôtit của gen * chiều dài trung bình của mỗi nuclêôtit = 200 * l

Vậy, khối lượng của gen là 200m và chiều dài của gen là 200l.

c) Để tính số nuclêôtit mỗi loại trong gen, ta cần biết tỷ lệ phần trăm của các loại nuclêôtit trong gen.

Với tỷ lệ phần trăm đã được tính ở câu a), ta có:

• Số nuclêôtit loại G: 5% của tổng số nuclêôtit của gen = 5% * 200 = 10
• Số nuclêôtit loại X: 5% của tổng số nuclêôtit của gen = 5% * 200 = 10
• Số nuclêôtit loại A: 45% của tổng số nuclêôtit của gen = 45% * 200 = 90
• Số nuclêôtit loại T: 45% của tổng số nuclêôtit của gen = 45% * 200 = 90

Vậy, số nuclêôtit mỗi loại trong gen là:

• G: 10
• X: 10
• A: 90
• T: 90

d) Để tính số liên kết hidro của gen, ta cần biết số liên kết hidro tạo thành giữa các loại nuclêôtit.

Trong gen, số liên kết hidro tạo thành giữa các loại nuclêôtit là:

• Số liên kết hidro giữa G và C (trong mạch thứ nhất): 10 (vì có 10 nuclêôtit loại G)
• Số liên kết hidro giữa X và Y (trong mạch thứ hai): 10 (vì có

Là đúng dữ chưa em?

\(c,\dfrac{3\sqrt{x}-6}{7\sqrt{x}-3}=\dfrac{1}{6}\left(dk:x\ge0,x\ne\dfrac{9}{49}\right)\)

\(\Leftrightarrow\dfrac{6\left(3\sqrt{x}-6\right)-7\sqrt{x}+3}{6\left(7\sqrt{x}-3\right)}=0\)

\(\Leftrightarrow18\sqrt{x}-36-7\sqrt{x}+3=0\)

\(\Leftrightarrow11\sqrt{x}=33\)

\(\Leftrightarrow\sqrt{x}=3\)

\(\Leftrightarrow x=9\left(tmdk\right)\)

Vậy \(S=\left\{9\right\}\)

\(d,\dfrac{2\sqrt{x}+1}{\sqrt{x}-3}=\dfrac{1}{3}\left(dk:x\ne9,x\ge0\right)\)

\(\Leftrightarrow\dfrac{3\left(2\sqrt{x}+1\right)-\sqrt{x}+3}{3\left(\sqrt{x}-3\right)}=0\)

\(\Leftrightarrow6\sqrt{x}+3-\sqrt{x}+3=0\)

\(\Leftrightarrow5\sqrt{x}=-6\)

\(\Leftrightarrow\sqrt{x}=-\dfrac{6}{5}\left(ktm\right)\)

Vậy \(S=\varnothing\)

\(\dfrac{3\sqrt{x}-6}{7\sqrt{x}-3}=\dfrac{1}{6}\left(x\ge0\right) \\ \Leftrightarrow6\left(3\sqrt{x}-6\right)=7\sqrt{x}-3\\ \Leftrightarrow18\sqrt{x}-36=7\sqrt{x}-3\\ \Leftrightarrow18\sqrt{x}-7\sqrt{x}=-3+36\\ \Leftrightarrow11\sqrt{x}=33\\ \Leftrightarrow\sqrt{x}=\dfrac{33}{11}=3\\ x=3^2=9\\ Vậy:S=\left\{9\right\}\)

giúp mình bài 3 với ạ

\(C=\sqrt{14-8\sqrt{3}}-\sqrt{21-12\sqrt{3}}\)

\(=\sqrt{2\left(7-4\sqrt{3}\right)}-\sqrt{12-2\cdot2\sqrt{3}\cdot3+9}\)

\(=\sqrt{2}\cdot\sqrt{4-2\cdot2\cdot\sqrt{3}+3}-\sqrt{\left(\sqrt{12}-3\right)^2}\)

\(=\sqrt{2}\cdot\sqrt{\left(2-\sqrt{3}\right)^2}-\left|2\sqrt{3}-3\right|\)

\(=\sqrt{2}\cdot\left|2-\sqrt{3}\right|-\left(2\sqrt{3}-3\right)\) (vì \(2\sqrt{3}-3>0\) )

\(=\sqrt{2}\cdot\left(2-\sqrt{3}\right)-2\sqrt{3}+3\) (vì \(2-\sqrt{3}>0\) )

\(=2\sqrt{2}-\sqrt{6}-2\sqrt{3}+3\)

điểm P đâu

 Gọi \(q_1,q_2,...,q_n\left(q_i\inℚ,\forall i=\overline{1,n}\right)\). Theo đề bài, ta có \(q_1q_2...q_n\inℤ\) và \(q_i+q_j\inℤ,\forall i\ne j;i,j=\overline{1,n}\). Không mất tính tổng quát, giả sử \(q_1< q_2< ...< q_n\)

 Ta thấy \(q_1+q_2\inℤ\) và \(q_2+q_3\inℤ\) nên \(q_1-q_3\inℤ\). Mà \(q_1+q_3\inℤ\) nên nếu ta đặt \(q_1-q_3=v\) và \(q_1+q_3=u\) với \(u,v\inℤ\) thì \(q_1=\dfrac{u+v}{2};q_3=\dfrac{u-v}{2}\). Do \(q_1+q_2=\dfrac{u+v+2q_2}{2}\) và \(q_3+q_2=\dfrac{u-v+2q_2}{2}\) cũng là các số nguyên, hơn nữa \(u-v\equiv u+v\left(mod2\right)\) nên ta chỉ cần suy ra \(u+v+2q_1⋮2\) hay \(u+v\) là số chẵn, cũng tức là \(q_1=\dfrac{u+v}{2}\) là số nguyên. Một cách tương tự, ta sẽ chứng minh được \(q_i\inℤ,\forall i=\overline{1,n}\) (đpcm)

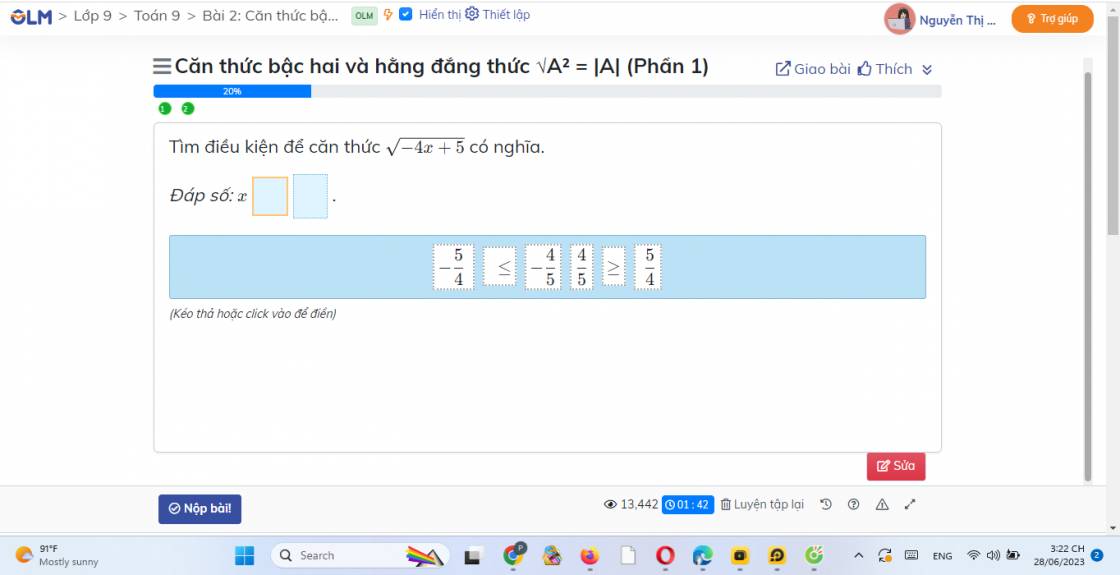
Câu c của em đấy nhé: \(\sqrt{-4x+5}\) có nghĩa ⇔ -4\(x\) + 5 ≥ 0 

                                                                                   4\(x\) ≤ 5 

                                                                                    \(x\) ≤ \(\dfrac{5}{4}\) 

Vậy em kéo dấu ≤ vào ô trống thứ nhất, sau đó em kéo \(\dfrac{5}{4}\) vào ô trống thứ hai rồi ấn nút nộp bài là xong em nhé

Aabb có TLGT là 1Ab:1ab

Nếu Aabb x kiểu gen chỉ cho 1 giao tử duy nhất sẽ cho mô hình phân li kiểu hình 1:1 

VD: Aabb x aabb hay Aabb x aaBB 

 Bài 1: Bài này số nhỏ nên chỉ cần chặn miền giá trị của \(x\) rồi xét các trường hợp thôi nhé. Ta thấy \(3^x< 35\Leftrightarrow x\le3\). Nếu \(x=0\) thì \(VT=2\), vô lí. Nếu \(x=1\) thì \(VT=5\), cũng vô lí. Nếu \(x=2\) thì \(VT=13\), vẫn vô lí. Nếu \(x=3\) thì \(VT=35\), thỏa mãn. Vậy, \(x=3\).

 Bài 2: Nếu \(x=0\) thì pt đã cho trở thành \(0!+y!=y!\Leftrightarrow0=1\), vô lí,

Nếu \(x=y\) thì pt trở thành \(2x!=\left(2x\right)!\) \(\Rightarrow\left(x+1\right)\left(x+2\right)...\left(2x\right)=2\) \(\Leftrightarrow x=1\Rightarrow y=1\)

Nếu \(x\ne y\) thì không mất tính tổng quát, giả sử \(1< y< x\) thì \(x!+y!< 2x!\le\left(x+1\right)x!=\left(x+1\right)!< \left(x+y\right)!\) nên pt đã cho không có nghiệm trong trường hợp này.

Như vậy, \(x=y=1\)

 Bài 3: Bổ sung đề là pt không có nghiệm nguyên dương nhé, chứ nếu nghiệm nguyên thì rõ ràng \(\left(x,y\right)=\left(0,19\right)\) là một nghiệm cũa pt đã cho rồi.

Giả sử pt đã cho có nghiệm nguyên dương \(\left(x,y\right)\)

Khi đó \(x,y< 19\). Không mất tính tổng quát ta có thể giả sử \(1< y\le x< 19\). Khi ấy \(x^{17}+y^{17}=19^{17}\ge\left(x+1\right)^{17}=x^{17}+17x^{16}+...>x^{17}+17x^{16}\), suy ra \(y^{17}>17x^{16}\ge17y^{16}\) \(\Rightarrow y>17\). Từ đó, ta thu được \(17< y\le x< 19\) nên \(x=y=18\). Thử lại thấy không thỏa mãn. 

Vậy pt đã cho không có nghiệm nguyên dương.

Chị độc giải sau khi em biết làm thôi à.