giúp mình với
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 3: 28 mét dây nặng số ki-lô-gam là:
0,5 x 28 : 4 = 3,5 (kg)
Kết luận: 28 mét dây nặng 3,5 kg

Ta có: \(5x=8y\)
hay \(\dfrac{x}{8}=\dfrac{y}{5}\)
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
\(\dfrac{x}{8}=\dfrac{y}{5}=\dfrac{y-x}{5-8}=\dfrac{-15}{-3}=5\)
Do đó:
\(\dfrac{x}{8}=5\Rightarrow x=8.5=40\)
\(\dfrac{y}{5}=5\Rightarrow y=5.5=25\)
Vậy \(x=40\); \(y=25\)
Ta có 5x = 8y
hay x/8 = y/5
Áp dụng tính chất dãy tỉ số bằng nhau, ta được:
x/8 = y/5 = y-x/5-8 = -15/-3=5
do đó:
x/8 = 5 suy ra x = 8,5 = 40
y/5 = 5 suy ra y = 5,5 = 25
Vậy x = 40, y = 25

\(\dfrac{x-3}{5-x}\) = \(\dfrac{5}{7}\) (đk \(x\) ≠ 5)
7.(\(x\) - 3) = 5.(5 - \(x\))
7\(x\) - 21 = 25 - 5\(x\)
7\(x\) + 5\(x\) = 25 + 21
12\(x\) = 46
\(x\) = 46 : 12
\(x\) = \(\dfrac{23}{6}\)
\(\dfrac{\left|x-2\right|}{2}\) = \(\dfrac{\left|2x+3\right|}{3}\)
3.|\(x\) - 2| = |2\(x\) + 3|.2
lập bảng ta có:
| \(x\) | - \(\dfrac{3}{2}\) 2 |
| 3.|\(x\) -2| | -3\(x\) + 6 3\(x\) - 6 0 3\(x\) - 6 |
| |2\(x\) + 3|.2 | -4\(x\) - 6 0 -4\(x\) - 6 0 4\(x\) + 6 |
Theo bảng trên ta có:
\(x\) < - \(\dfrac{3}{2}\) ⇒ -3\(x\) + 6 = - 4\(x\) - 6
-\(3x\) + 4\(x\) = - 6 - 6
\(x\) = -12
- \(\dfrac{3}{2}\) < \(x\) < 2 ⇒ 3\(x\) - 6 = - 4\(x\) - 6
3\(x\) + 4\(x\) = 6 - 6
7\(x\) = 0
\(x\) = 0
2 < \(x\) ⇒ 3\(x\)- 6 = 4\(x\) + 6
4\(x\) - 3\(x\) = - 6 - 6
\(x\) = -12 (loại)
Vậy \(x\) \(\in\) {-12; 0}

Đề mờ quá. Bạn nên gõ hẳn đề ra để mọi người hỗ trợ tốt hơn nhé.


a) Thể tích hồ bơi:
12,5 . 5 . 2,5 = 156,25 (m³)
b) Diện tích đáy hồ bơi:
12,5 . 5 = 62,5 (m²)
Diện tích xung quanh hồ bơi:
(12,5 + 5) . 2 . 2,5 = 87,5 (m²)
Diện tích cần lát gạch:
87,5 + 62,5 = 150 (m²)
c) Thể tích nước trong hồ bơi:
12,5 . 5 . 1,5 = 93,75 (m³)
`#3107.101107`
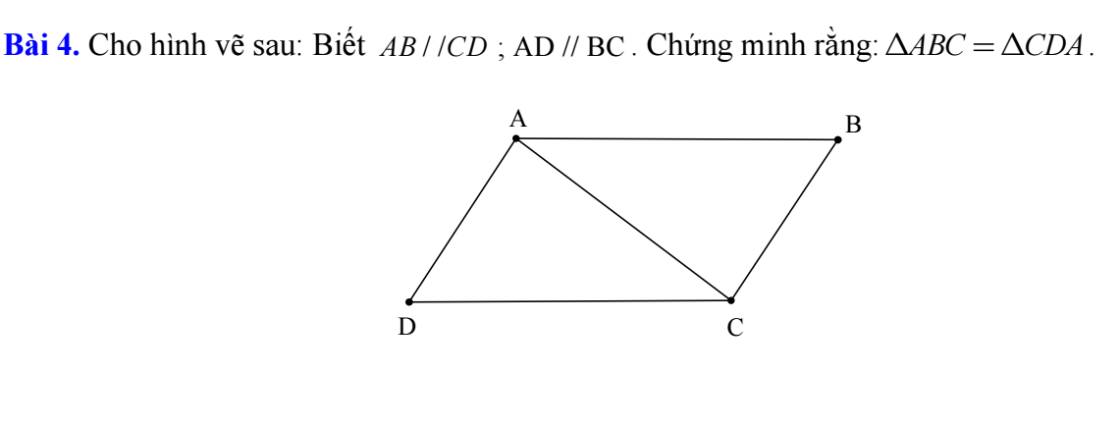
Ta có: `\text{AB // CD}`
\(\Rightarrow\) \(\widehat{\text{BAC}}=\widehat{\text{DCA}}\)
Vì `\text{AD // BC}`
\(\Rightarrow\widehat{\text{DAC}}=\widehat{\text{BCA}}\)
Xét `\Delta ABC` và `\Delta CDA` :
\(\widehat{\text{BAC}}=\widehat{\text{DCA}}\)
\(\text{AC chung}\)
\(\widehat{\text{DAC}}=\widehat{\text{BCA}}\)
\(\Rightarrow\Delta\text{ABC = }\Delta\text{CDA (g - c - g).}\)