 Giúp mình hết vs ạ cảm ơn mn nhiu
Giúp mình hết vs ạ cảm ơn mn nhiu
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Câu 25:
Sửa đề: \(\dfrac{2}{1\cdot3}+\dfrac{2}{3\cdot5}+...+\dfrac{2}{2021\cdot2023}\)
\(=1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+...+\dfrac{1}{2021}-\dfrac{1}{2023}\)
\(=1-\dfrac{1}{2023}=\dfrac{2022}{2023}\)
Câu 23:
Số học sinh nam là:
\(45\cdot\dfrac{2}{3+2}=45\cdot\dfrac{2}{5}=18\left(bạn\right)\)
Số học sinh nữ là 45-18=27(bạn)


Số dư không lớn hơn số chia nên số dư lớn nhất là:
\(49-1=48\)
Số bị chia là:
\(272\times49+48=13376\)
Đáp số: 13376
Số dư nhỏ hơn số chia nên số dư lớn nhất là:
\(49-1=48\)
Số bị chia là:
\(272\times49-48=13376\)
Đáp số: 13 376


\(3\left(x-2\right)=-100+211\\ 3\left(x-2\right)=111\\ x-2=37\\ x=39.\)
`#3107.101107`
`3(x - 2) = -100 + 211`
`\Rightarrow 3(x - 2) = 111`
`\Rightarrow x - 2 = 111 \div 3`
`\Rightarrow x - 2 = 37`
`\Rightarrow x = 37 + 2`
`\Rightarrow x = 39`
Vậy, `x = 39.`

Số tự nhiên lớn nhất có bốn chữ số mà trong đó không có hai chữ số nào giống nhau là: 9876

Ta có: \(E=\dfrac{1}{3}+\dfrac{2}{3^2}+\dfrac{3}{3^3}+...+\dfrac{100}{3^{100}}\)
\(3E=1+\dfrac{2}{3}+\dfrac{3}{3^2}+...+\dfrac{100}{3^{99}}\)
\(3E-E=\left(1+\dfrac{2}{3}+\dfrac{3}{3^2}+..+\dfrac{100}{3^{99}}\right)-\left(\dfrac{1}{3}+\dfrac{2}{3^2}+\dfrac{3}{3^3}+...+\dfrac{100}{3^{100}}\right)\)
\(2E=1+\dfrac{1}{3}+\dfrac{1}{3^3}+...+\dfrac{1}{3^{99}}-\dfrac{100}{3^{100}}\)
\(6E=3+1+\dfrac{1}{3^2}+...+\dfrac{1}{3^{98}}-\dfrac{100}{3^{99}}\)
\(6E-2E=\left(3+1+\dfrac{1}{3^2}+...+\dfrac{1}{3^{98}}-\dfrac{100}{3^{99}}\right)-\left(1+\dfrac{1}{3}+\dfrac{1}{3^3}+...+\dfrac{1}{3^{99}}-\dfrac{100}{3^{100}}\right)\)
\(4E=3-\dfrac{100}{3^{99}}-\dfrac{100}{3^{100}}\)
\(\Rightarrow E=\dfrac{3-\dfrac{100}{3^{99}}-\dfrac{100}{3^{100}}}{4}=\dfrac{3}{4}-\dfrac{\dfrac{100}{3^{99}}+\dfrac{100}{3^{100}}}{4}< \dfrac{3}{4}\) (đpcm)

Bài 1:
a; \(\dfrac{1}{n}\); \(\dfrac{1}{n+1}\) (n > 0; n \(\in\) Z)
\(\dfrac{1}{n}\) - \(\dfrac{1}{n+1}\) = \(\dfrac{n+1-1}{n.\left(n+1\right)}\) = \(\dfrac{1}{n\cdot\left(n+1\right)}\)
⇒ \(\dfrac{1}{n}\) - \(\dfrac{1}{n+1}\) = \(\dfrac{1}{n\left(n+1\right)}\) (đpcm)
Bài 1b
A = \(\dfrac{1}{2.3}\) + \(\dfrac{1}{3.4}\) + \(\dfrac{1}{4.5}\) + \(\dfrac{1}{5.6}\) + \(\dfrac{1}{6.7}\) + \(\dfrac{1}{7.8}\) + \(\dfrac{1}{8.9}\)
A = \(\dfrac{1}{2}\) - \(\dfrac{1}{3}\) + \(\dfrac{1}{3}\) - \(\dfrac{1}{4}\) + \(\dfrac{1}{4}\) - \(\dfrac{1}{5}\) +\(\dfrac{1}{5}\) - \(\dfrac{1}{6}\) + \(\dfrac{1}{6}\) - \(\dfrac{1}{7}\) + \(\dfrac{1}{7}\) - \(\dfrac{1}{8}\) + \(\dfrac{1}{8}\) - \(\dfrac{1}{9}\)
A = \(\dfrac{1}{2}\) - \(\dfrac{1}{9}\)
A = \(\dfrac{7}{18}\)



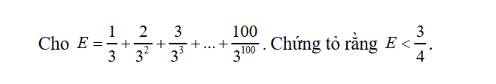

a, A = { n \(\in N\)| 1 =< n =< 5 }
b, B = { n \(\in\)N| 0 =< n =< 4 }
c, C = { n \(\in N\)| 1 =< n =< 4 }
d, D = { \(n\in N\)| 0 =< n =< 3, 2n+2 }
e, E = { \(n\in\)N| 0 =< n =< 24, 2n+1 }
f, F = { n \(\in\)N| 1 =< n =< 9, 11n }
Bài 2:
a) \(A=\left\{x\in N|1\le x\le5\right\}\)
b) \(B=\left\{x\in N|0\le x\le4\right\}\)
c) \(C=\left\{x\in N|1\le x\le4\right\}\)
d) \(D=\left\{x=2k|k\in N;0\le k\le4\right\}\)
e) \(E=\left\{x=2k+1|k\in N;0\le k\le21\right\}\)
f) \(F=\left\{x=11k|k\in N;1\le k\le9\right\}\)