b) Do ∆ABD = ∆AID (cmt)

⇒ DB = ID (hai cạnh tương ứng)

∆ICD vuông tại I

⇒ DC là cạnh huyền nên là cạnh lớn nhất

⇒ ID < DC

Mà DB = ID (cmt)

⇒ DB < DC

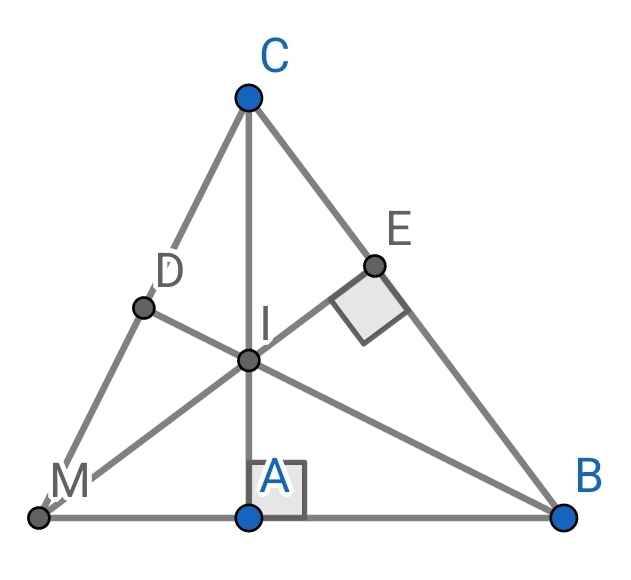
a) Xét hai tam giác vuông: ∆ABI và ∆EBI có:

BI là cạnh chung

BA = BE (gt)

⇒ ∆ABI = ∆EBI (cạnh huyền - cạnh góc vuông)

b) Do ∆ABI = ∆EBI (cmt)

⇒ AI = EI (hai cạnh tương ứng)

Xét hai tam giác vuông: ∆IAM và ∆IEC có:

AI = EI (cmt)

∠AIM = ∠EIC (đối đỉnh)

⇒ ∆IAM = ∆IEC (cạnh góc vuông - góc nhọn kề)

⇒ AM = EC (hai cạnh tương ứng)

c) ∆ABC vuông tại A (gt)

⇒ CA ⊥ AB

⇒ CA ⊥ BM

⇒ CA là đường cao của ∆BCM

Do IE ⊥ BC (gt)

⇒ ME ⊥ BC

⇒ ME là đường cao thứ hai của ∆BCM

Mà ME và CA cắt nhau tại I

⇒ I là trực tâm của ∆BCM

⇒ BI ⊥ CM

Ta có:

BE = BA (gt)

CE = AM (cmt)

⇒ BE + CE = BA + AM

⇒ BC = BM

⇒ ∆BCM cân tại B

Mà D là trung điểm của MC (gt)

⇒ BD là đường trung tuyến của ∆BCM

⇒ BD cũng là đường cao của ∆BCM

⇒ BD ⊥ CM

Mà BI ⊥ CM (cmt)

⇒ B, I, D thẳng hàng

a) Ta có:

• ∠BAE = ∠BEA (vì BE = BA)
• ∠BAE + ∠BEA = 90° (vì AE vuông góc với BC) => ∠BAE = ∠BEA = 45°

Vậy ∆BAI và ∆BEI là hai tam giác cân có cạnh góc vuông, do đó chúng là hai tam giác đồng dạng. => ∆ABI = ∆EBI (theo tính đồng dạng của hai tam giác).

b) Ta có:

• ∠BAE = 45° (vì BE = BA và AE vuông góc với BC)
• ∠BAM = 90° (vì AM vuông góc với BC)

Vậy ∠BAE = ∠BAM. => Tam giác ∆BAE đồng dạng với tam giác ∆BAM (theo góc bên trong tương đương của tam giác đồng dạng). => AM = EC (theo tính chất của tam giác đồng dạng, tỉ lệ các cạnh tương ứng).

c) Gọi D là trung điểm của MC. Ta có:

• D là trung điểm của MC => DM = DC.
• ∠BEC = 90° (vì BE vuông góc với EC) => ∆BED và ∆BDM là hai tam giác vuông cân (vì BE = BA và BD = DM). => ∠BED = ∠BMD = 45° (vì BD cắt BE và DM cắt EC tại góc vuông). => ∠BID = 90° (vì BD vuông góc với BI) => ∠BID = ∠BED + ∠BMD = 45° + 45° = 90°.

Vậy ba điểm B, I, D thẳng hàng.

B nha 

Hoctot!

Cho đa thức P(x) = 0

=) \(2x-\dfrac{1}{3}=0\)

    \(2x=\dfrac{1}{3}\)

    \(x=\dfrac{1}{3}:2\)

    \(x=6\)

Đáp án : B

Để phân biệt nghĩa của các yếu tố cấu tạo Hán Việt đồng âm trong các từ Hán Việt đã cho, ta có thể dựa vào ngữ cảnh và ý nghĩa cụ thể của từng từ. Dưới đây là cách phân biệt:

a) Trang:

• Trang điểm: việc làm đẹp cho khuôn mặt hoặc cơ thể bằng mỹ phẩm.
• Trang sức: các vật dụng làm đẹp cho cơ thể như vòng cổ, nhẫn, bạc trang sức.
• Trang trí: việc trang trí, làm đẹp cho không gian hoặc vật dụng.
• Trang hoàng: việc trang trí, làm đẹp cho không gian hoặc sự kiện.
• Trang phục: quần áo, trang sức mà một người mặc.

b) Sinh:

• Sinh thành: quá trình ra đời của một sinh vật.
• Sinh trưởng: quá trình phát triển và lớn lên của một sinh vật.
• Sơ sinh: trạng thái của trẻ em ngay sau khi ra đời.
• Phát sinh: sự xuất hiện, sự xảy ra của một sự kiện mới.

c) Trách:

• Oán trách: sự trách móc, quở trách.
• Khiển trách: sự chỉ trích, quở trách.
• Trách cứ: lời trách móc, lời quở trách.

d) Thương:

• Thương mại: hoạt động buôn bán hàng hóa, dịch vụ.
• Nội thương: kinh doanh trong nước.
• Ngoại thương: kinh doanh quốc tế.
• Gian thương: nỗi đau khổ, sự thương tâm.

e) Sĩ:

• Sĩ phu: người học trò trong thời phong kiến.
• Nữ sĩ: phụ nữ có học thức, tri thức.
• Tiến sĩ: người đã đạt được học vị cao nhất trong một lĩnh vực.
• Sĩ tử: học sinh, sinh viên.

g) Quan:

• Quan sát: hành động theo dõi, theo sát một sự vật, hiện tượng.
• Quan điểm: quan niệm, quan điểm cá nhân về một vấn đề nào đó.
• Bàng quan: sự khách quan, không chủ quan.
• Bi quan: tình trạng nhìn nhận mọi việc theo hướng tiêu cực.

Thông qua các định nghĩa trên, bạn có thể phân biệt được ý nghĩa của các từ đồng âm trong câu hỏi.

câu d (x-y)² nha mn

Chọn C

Trong tư duy của một số người, có một niềm tin rằng sự giàu có về trí tuệ có thể tự nhiên đi kèm với một số lượng đáng kể của giàu có về nhân cách. Tuy nhiên, có những quan điểm khác nhau về mối quan hệ giữa sự giàu có về trí tuệ và giàu có về nhân cách.

Theo quan điểm của một số người, sự giàu có về trí tuệ có thể đóng vai trò quan trọng trong việc phát triển nhân cách. Sự thông minh, kiến thức và kỹ năng có thể giúp một người hiểu biết và tư duy về thế giới xung quanh, từ đó phát triển sự thông thái, sự hiểu biết, và sự empati. Có thể nói rằng sự giàu có về trí tuệ có thể là một yếu tố quan trọng trong việc xây dựng một nhân cách đa chiều và phong phú.

Tuy nhiên, không phải lúc nào sự giàu có về trí tuệ cũng đi đôi với giàu có về nhân cách. Một người có thể có kiến thức và trí tuệ rộng lớn, nhưng vẫn thiếu đi tính nhân văn, sự tử tế và lòng tốt. Sự giàu có về nhân cách không chỉ đánh giá qua hành động và cử chỉ bên ngoài, mà còn là về tính cách, giá trị và lòng trung thành. Một người giàu có về nhân cách thường là người có lòng tốt, sẵn lòng giúp đỡ và chia sẻ với người khác, và có khả năng xây dựng mối quan hệ tốt đẹp với những người xung quanh.

Vì vậy, dù sự giàu có về trí tuệ có thể mang lại một lợi thế trong nhiều lĩnh vực của cuộc sống, nhưng không thể bỏ qua tầm quan trọng của sự giàu có về nhân cách. Đối với một cuộc sống hạnh phúc và ý nghĩa, việc cân nhắc và phát triển cả hai mặt này là quan trọng.

a: Xét ΔMAB và ΔMCD có

MA=MC

\(\widehat{AMB}=\widehat{CMD}\)(hai góc đối đỉnh)

MB=MD

Do đó: ΔMAB=ΔMCD

b: Xét ΔCBD có

CM,DN là các đường trung tuyến

CM cắt DN tại G

Do đó: G là trọng tâm của ΔCDB

a: ΔABC vuông tại A

=>\(\widehat{ABC}+\widehat{ACB}=90^0\)

=>\(\widehat{ACB}=90^0-60^0=30^0\)

b: Xét ΔBAE vuông tại A và ΔBHE vuông tại H có

BE chung

BA=BH

Do đó: ΔBAE=ΔBHE

=>\(\widehat{ABE}=\widehat{HBẺ}\)

=>BE là phân giác của góc ABC

c: Xét ΔBKC có

KH,CA là các đường cao

KH cắt CA tại E

Do đó: E là trực tâm của ΔBKC

=>BE\(\perp\)KC

a) Tính góc C: Vì tam giác ABC vuông tại A và góc B = 60 độ, ta có góc C = 90 - 60 = 30 độ.

b) Chứng minh BE là tia phân giác của góc B: Gọi I là trung điểm của AB, vậy BI là đoạn thẳng phân giác của góc B. Ta có HB = AB và BI là đoạn thẳng phân giác của góc B, do đó tam giác BHI là tam giác đều. Do đó, góc BHI = 60 độ. Mà góc HBE là góc ngoài của tam giác BHI, vậy góc HBE = 60 độ. Vậy, BE là tia phân giác của góc B.

c) Chứng minh rằng BE vuông góc với KC: Ta có:

• Tam giác ABC vuông tại A.
• Tam giác BHI đều. Vậy ta có:
• AH là đường cao của tam giác ABC, vì vậy HK là đường cao của tam giác BHI.
• BK là cạnh của tam giác BHI. Vậy tam giác BKH là tam giác vuông tại K.

Vậy góc HKB = 90 độ.

Nhưng ta đã chứng minh BE là tia phân giác của góc B, vậy góc HBE = góc EBK.

Vậy ta có: góc EBK + góc HKB = góc HBE + góc HKB = 60 + 90 = 150 độ.

Nhưng tổng các góc trong tam giác BKH là 180 độ, vậy góc EBK + góc HKB = 180 độ.

Từ đó suy ra góc EBK = 30 độ.

ΔAED vuông tại E

=>AE<AD

ΔCFD vuông tại F

=>CF<CD

AE<AD

CF<CD

Do đó: AE+CF<AD+CD=AC

Không có a và b thỏa mãn đề bài