 giup em 2 bai nay em cam on a
giup em 2 bai nay em cam on a
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: \(\dfrac{2}{5}\cdot4-\dfrac{3}{5}\cdot7\cdot\dfrac{3}{2}\)
\(=\dfrac{8}{5}-\dfrac{63}{10}\)
\(=\dfrac{16}{10}-\dfrac{63}{10}=-\dfrac{47}{10}\)
b: \(-\dfrac{21}{10}+\dfrac{21}{10}\cdot\dfrac{3}{4}-\dfrac{3}{4}\)
\(=\dfrac{-21}{10}\left(1-\dfrac{3}{4}\right)-\dfrac{3}{4}\)
\(=-\dfrac{21}{10}\cdot\dfrac{1}{4}-\dfrac{3}{4}=\dfrac{-21}{40}-\dfrac{3}{4}=\dfrac{-51}{40}\)
c: \(\dfrac{-2}{5}\cdot\left(-6\right)+\dfrac{3}{4}\cdot\dfrac{4}{-10}\)
\(=\dfrac{12}{5}-\dfrac{3}{10}\)
\(=\dfrac{24}{10}-\dfrac{3}{10}=\dfrac{21}{10}\)
a)2/5.4-3/5.7.3/2 b)-21/10 + 21/10 . 3/4-34
=8/5-63/10 =-21/10 +(21/10 . 3/4) -3/4
=-47/10 =-21/10+63/40-3/4
=-56/40

\(A=\dfrac{2}{1\cdot3}+\dfrac{2}{3\cdot5}+\dfrac{2}{5\cdot7}+\dots+\dfrac{2}{99\cdot101}\)
\(=1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+\dots+\dfrac{1}{99}-\dfrac{1}{101}\)
\(=1-\dfrac{1}{101}=\dfrac{100}{101}\)


\(\dfrac{3}{13}\cdot\dfrac{6}{11}+\dfrac{3}{13}-\dfrac{9}{11}\cdot\dfrac{9}{11}-\dfrac{3}{13}\cdot\dfrac{4}{11}\)
\(=\dfrac{3}{13}\left(\dfrac{6}{11}+1-\dfrac{4}{11}\right)-\dfrac{81}{121}\)
\(=\dfrac{3}{13}\cdot\dfrac{13}{11}-\dfrac{81}{121}\)
\(=\dfrac{3}{11}-\dfrac{81}{121}=-\dfrac{48}{121}\)

a/Lãi suất tiết kiệm:
\(6030000:6000000-100\%=0,005=0,5\%\)
b/Số tiền gốc và lãi rút ra được tất cả trong 2 tháng:
\(6030000+6030000\cdot0,5\%=6060150\left(đ\right)\)
a,Lãi Suất là:
[6030000-6000000]:6000000 nhân 100=0,5 phần trăm
b,Số tiền lãi sau 22 tháng là :
30000.0,5=6000030000.0,5=60000 ( đồng )
Trong 22 tháng thì rút ra tiền gốc và lãi được tất cả số tiền là :
6000000+60000=60600006000000+60000=6060000 ( đồng )

\(\dfrac{1}{2}+\dfrac{1}{6}+...+\dfrac{1}{10100}\)
\(=\dfrac{1}{1\cdot2}+\dfrac{1}{2\cdot3}+...+\dfrac{1}{100\cdot101}\)
\(=1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{100}-\dfrac{1}{101}\)
\(=1-\dfrac{1}{101}=\dfrac{100}{101}\)

a: \(\dfrac{-14}{21}< 0\)
\(\dfrac{-60}{-72}=\dfrac{60}{72}>0\)
Do đó: \(\dfrac{-14}{21}< \dfrac{-60}{-72}\)
a) Ta có \(\dfrac{-60}{-72}\)=\(\dfrac{60}{72}\)
Vì \(\dfrac{-14}{21}\) < 0 Mà \(\dfrac{-60}{-72}\)=\(\dfrac{60}{72}\) > 0
=> \(\dfrac{60}{72}\) > \(\dfrac{-14}{21}\) => \(\dfrac{-60}{-72}\) >\(\dfrac{-14}{21}\)
Vậy \(\dfrac{-60}{-72}\) > \(\dfrac{-14}{21}\)
b)
+) Ta có BCNN(24,18) = 72
+) 72 : 24 = 3
72 : 18 = 4
+)\(\dfrac{5}{24}\) = \(\dfrac{5.3}{24.3}\) = \(\dfrac{15}{72}\)
\(\dfrac{7}{18}\) = \(\dfrac{7.4}{18.4}\) = \(\dfrac{28}{72}\)
+) Vì 15 < 28 nên \(\dfrac{15}{72}\) < \(\dfrac{28}{72}\) => \(\dfrac{5}{24}\) < \(\dfrac{7}{18}\)
Vậy \(\dfrac{5}{24}\) < \(\dfrac{7}{18}\)

\(S=5+5^2+...+5^{2024}\)
\(=\left(5+5^2+5^3+5^4\right)+\left(5^5+5^6+5^7+5^8\right)+...+\left(5^{2021}+5^{2022}+5^{2023}+5^{2024}\right)\)
\(=\left(5+5^2+5^3+5^4\right)+5^4\left(5+5^2+5^3+5^4\right)+...+5^{2020}\left(5+5^2+5^3+5^4\right)\)
\(=780\left(1+5^4+...+5^{2020}\right)⋮780\)
=>\(S⋮65\)
Số số hạng của S:
2024 - 1 + 1 = 2024 số hạng
Do 2024 ⋮ 4 nên ta có thể nhóm các số hạng của S thành từng nhóm mà mỗi nhóm có 4 số hạng như sau:
S = (5 + 5² + 5³ + 5⁴) + (5⁵ + 5⁶ + 5⁷ + 5⁸) + ... + (5²⁰²¹ + 5²⁰²² + 5²⁰²³ + 5²⁰²⁴)
= 780 + 5⁴.(5 + 5² + 5³ + 5⁴) + ... + 5²⁰²⁰.(5 + 5² + 5³ + 5⁴)
= 780 + 5⁴.780 + ... + 5²⁰²⁰.780
= 780.(1 + 5⁴ + ... + 5²⁰²⁰)
= 65.12.(1 + 5⁴ + ... + 5²⁰²⁰) ⋮ 65
Vậy S ⋮ 65
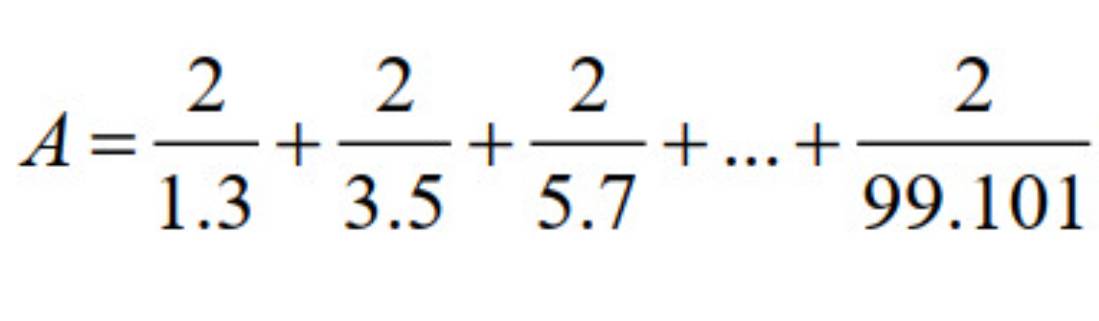
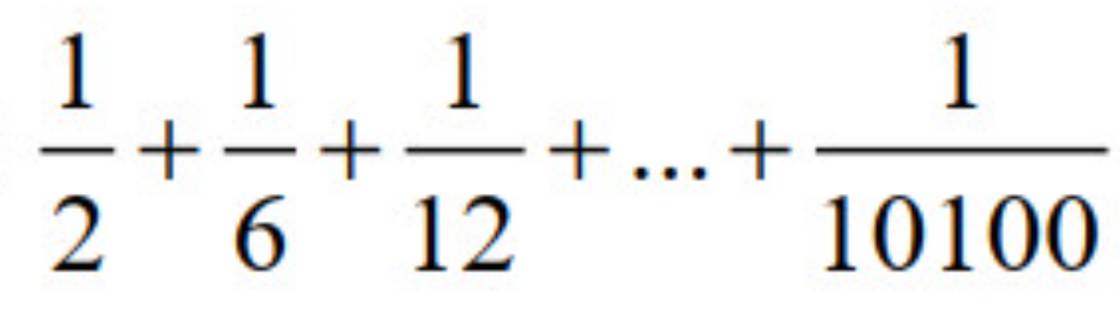
Bài 10:
Số học sinh giỏi ngoại ngữ chiếm:
\(\dfrac{1}{3}:\dfrac{4}{5}=\dfrac{1}{3}\cdot\dfrac{5}{4}=\dfrac{5}{12}\)(tổng số học sinh)
Số học sinh giỏi Văn là:
\(1-\dfrac{1}{3}-\dfrac{5}{12}=\dfrac{12-4-5}{12}=\dfrac{3}{12}=\dfrac{1}{4}\)(tổng số học sinh)
Tổng số học sinh là: \(6:\dfrac{1}{4}=24\left(bạn\right)\)
Số học sinh giỏi toán là \(24\cdot\dfrac{1}{3}=8\left(bạn\right)\)
Số học sinh giỏi ngoại ngữ là 24-8-6=10(bạn)
Bài 11:
a: Để A là phân số thì \(x+2\ne0\)
=>\(x\ne-2\)
b: Để A là số nguyên thì \(2x-1⋮x+2\)
=>\(2x+4-5⋮x+2\)
=>\(-5⋮x+2\)
=>\(x+2\in\left\{1;-1;5;-5\right\}\)
=>\(x\in\left\{-1;-3;3;-7\right\}\)