Trước nguy cơ cuộc khởi nghĩa bị tan rã, Nguyễn Chích - một tướng của nghĩa quân Lam Sơn đã hiến kế: “Nghệ An là nơi hiểm, yếu, đất rộng, người đông, tôi đã từng qua lại Nghệ An, nên rất thông thuộc đường đất.

Trong truyện ngụ ngôn "Con lừa già và người nông dân", một đặc điểm nổi bật là việc sử dụng các nhân vật động vật để ẩn dụ cho hành vi và tính cách con người. Truyện kể về một con lừa già không còn khả năng làm việc nặng như trước, và người nông dân quyết định không cho nó ăn nữa với hy vọng rằng con lừa sẽ chết. Tuy nhiên, con lừa đã tìm cách cứu mình bằng cách giả vờ chết để thoát khỏi sự ngược đãi của người nông dân.

Trong truyện này, con lừa tượng trưng cho những cá nhân già cỗi, bị xã hội bỏ rơi khi họ không còn khả năng đóng góp. Người nông dân đại diện cho những người lạm dụng và không trân trọng những đóng góp trước đây của người khác khi họ không còn hữu ích. Sử dụng nhân vật động vật thay cho con người giúp đơn giản hóa các bài học đạo đức và làm cho chúng dễ tiếp cận hơn với độc giả, đồng thời cung cấp một cái nhìn sâu sắc về những khuyết điểm của xã hội con người mà không trực tiếp chỉ trích bất kỳ cá nhân cụ thể nào. Truyện ngụ ngôn như vậy thường mang đến bài học hoặc đạo lý thông qua câu chuyện hấp dẫn và tượng trưng.

Quan điểm của em về ý kiến "học sinh có thể thường xuyên chơi các trò chơi điện tử" là cần cân nhắc và có sự điều chỉnh. Việc chơi trò chơi điện tử có thể mang lại một số lợi ích như giải trí, giảm căng thẳng và phát triển kỹ năng tư duy. Tuy nhiên, việc chơi quá nhiều và thường xuyên có thể gây ra một số vấn đề đáng lo ngại.
Trước hết, việc chơi trò chơi điện tử quá nhiều có thể ảnh hưởng đến hiệu suất học tập của học sinh. Thời gian dành cho trò chơi có thể làm giảm thời gian học tập và làm bài tập, dẫn đến kết quả học tập không tốt và ảnh hưởng đến sự phát triển học thuật của họ.
Thứ hai, việc chơi trò chơi điện tử quá mức có thể gây ra các vấn đề về sức khỏe, như mất ngủ, cận thị, và thậm chí là béo phì. Điều này đặc biệt đáng lo ngại đối với trẻ em và thanh thiếu niên, khi cơ thể của họ đang phát triển và cần thời gian vàng để vận động và phát triển một cách lành mạnh.
Cuối cùng, việc chơi trò chơi điện tử quá mức có thể gây ra sự cô lập và thiếu giao tiếp xã hội. Khi học sinh dành quá nhiều thời gian trên các thiết bị điện tử, họ có thể ít tiếp xúc và giao tiếp với bạn bè và gia đình, điều này có thể ảnh hưởng đến mối quan hệ xã hội và tinh thần của họ.
Việc chơi các trò chơi điện tử có thể mang lại một số lợi ích, nhưng cần phải có sự cân nhắc và kiểm soát để tránh các tác động tiêu cực đến hiệu suất học tập, sức khỏe và mối quan hệ xã hội của học sinh.

a: Xét ΔNMI vuông tại M và ΔNKI vuông tại K có

NI chung

\(\widehat{MNI}=\widehat{KNI}\)

Do đó: ΔNMI=ΔNKI

b: ta có: ΔNMI=ΔNKI

=>IM=IK

mà IK<IP(ΔIKP vuông tại K)

nên IM<IP

c: Xét ΔIMQ vuông tại M và ΔIKP vuông tại K có

IM=IK

\(\widehat{MIQ}=\widehat{KIP}\)(hai góc đối đỉnh)

Do đó: ΔIMQ=ΔIKP

=>IQ=IP

=>ΔIQP cân tại I

Xét ΔNQP có

QK,PM là các đường cao

QK cắt PM tại I

Do đó: I là trực tâm của ΔNQP

=>NI\(\perp\)PQ tại D

=>ND\(\perp\)PQ

MI < IP mà

a: ΔABC vuông tại A

=>\(\widehat{ABC}+\widehat{ACB}=90^0\)

=>\(\widehat{ACB}=90^0-60^0=30^0\)

Xét ΔABC có \(\widehat{ACB}< \widehat{ABC}< \widehat{BAC}\)

mà AB,AC,BC lần lượt là cạnh đối diện của các góc ACB,ABC,BAC

nên AB<AC<BC

b: Xét ΔBAE vuông tại A và ΔBHE vuông tại H có

BE chung

\(\widehat{ABE}=\widehat{HBE}\)

Do đó: ΔBAE=ΔBHE

c: ΔBAE=ΔBHE

=>BA=BH

Xét ΔBHK vuông tại H và ΔBAC vuông tại A có

BH=BA

\(\widehat{HBK}\) chung

Do đó: ΔBHK=ΔBAC

=>BK=BC

=>ΔBKC cân tại B

Xét ΔBKC cân tại B có \(\widehat{KBC}=60^0\)

nên ΔBKC đều

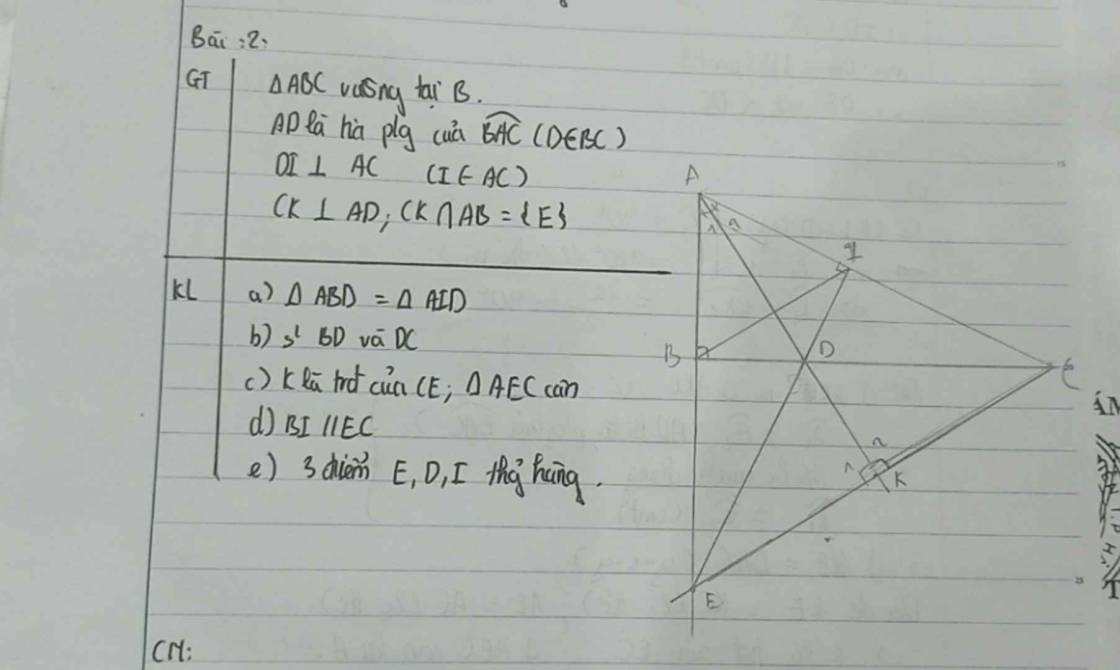
a: Xét ΔABD vuông tại B và ΔAID vuông tại I có

AD chung

\(\widehat{BAD}=\widehat{IAD}\)

Do đó: ΔABD=ΔAID

b: ta có: ΔABD=ΔAID

=>DB=DI

mà DI<DC(ΔDIC vuông tại I)

nên DB<DC

c: Xét ΔAEC có

AK là đường cao

AK là đường phân giác

Do đó: ΔAEC cân tại A

Ta có: ΔAEC cân tại A

mà AK là đường cao

nên K là trung điểm của EC

d: Xét ΔAEC có \(\dfrac{AB}{AE}=\dfrac{AI}{AC}\)

nên BI//EC

e: Xét ΔAEC có

AK,CB là các đường cao

AK cắt CB tại D

Do đó: D là trực tâm của ΔAEC

=>ED\(\perp\)AC

mà DI\(\perp\)AC

và ED,DI có điểm chung là D

nên E,D,I thẳng hàng

a: Xét ΔNMD vuông tại M và ΔNED vuông tại E có

ND chung

\(\widehat{MND}=\widehat{END}\)

Do đó: ΔNMD=ΔNED
b: Ta có; ΔNMD=ΔNED

=>DM=DE

Xét ΔDMF vuông tại M và ΔDEP vuông tại E có

DM=DE
\(\widehat{MDF}=\widehat{EDP}\)

Do đó: ΔDMF=ΔDEP

=>DF=DP

=>ΔDFP cân tại D

c: Ta có: ΔDMF=ΔDEP

=>MF=EP

ΔNMD=ΔNED
=>NM=NE

Ta có: NM+MF=NF

NE+EP=NP

mà NM=NE và MF=EP

nên NF=NP

=>N nằm trên đường trung trực của FP(1)

Ta có: DF=DP

=>D nằm trên đường trung trực của FP(2)

Ta có: KF=KP

=>K nằm trên đường trung trực của FP(3)

Từ (1),(2),(3) suy ra N,D,K thẳng hàng

Bài 5:

a: Xét ΔABC có \(\widehat{BAC}+\widehat{ABC}+\widehat{ACB}=180^0\)

=>\(\widehat{ACB}+57^0+72^0=180^0\)

=>\(\widehat{ACB}=51^0\)

Xét ΔABC có \(\widehat{ACB}< \widehat{BAC}< \widehat{ABC}\)

mà AB,BC,AC lần lượt là cạnh đối diện của các góc ACB,BAC,ABC

nên AB<BC<AC

b: Xét ΔBIM và ΔCEM có

MB=MC

\(\widehat{BMI}=\widehat{CME}\)(hai góc đối đỉnh)

MI=ME

Do đó: ΔBIM=ΔCEM

=>\(\widehat{BIM}=\widehat{CEM}\)

=>BI//CE

c: Xét ΔMAK có

MH là đường cao

MH là đường trung tuyến

Do đó: ΔMAK cân tại M

Bài 6:

Số tiền của hóa đơn sau khi giảm giá lần 1 là:

\(16,245:\left(1-5\%\right)=17,1\left(triệuđồng\right)\)

Số tiền đúng của hóa đơn ban đầu là:

17,1:(1-10%)=19(triệu đồng)

Giá niêm yết của cái tivi là:

19-7=12(triệu đồng)

a: Xét ΔBHA và ΔBHD có

BH chung

HA=HD

BA=BD

Do đó: ΔBHA=ΔBHD

b: ΔBHA=ΔBHD

=>\(\widehat{ABH}=\widehat{DBH}\)

Xét ΔBAE và ΔBDE có

BA=BD

\(\widehat{ABE}=\widehat{DBE}\)

BE chung

Do đó: ΔBAE=ΔBDE
=>EA=ED
=>ΔEAD cân tại E

c: Xét ΔADF có HE//DF

nên \(\dfrac{HE}{DF}=\dfrac{AH}{AD}=\dfrac{1}{2}\)

Xét ΔKDF và ΔKEH có

\(\widehat{KDF}=\widehat{KEH}\)(DF//EH)

\(\widehat{DKF}=\widehat{EKH}\)(hai góc đối đỉnh)

Do đó: ΔKDF~ΔKEH

=>\(\dfrac{KD}{KE}=\dfrac{DF}{EH}=2\)

=>KD=2KE