Mình nghĩ là bằng nhau.

`060° = 60°`nhé

-> You are not allowed to smoke in this restaurant.

-> You should not have entered my room without asking me first.

-> Will you be able to participate in the race next Thursday?

=> You are not allowed to smoke in this restaurant.

=> You should have asked me first before coming into my room.

=> Will you be able to take part in the race next Thursday?

1: BC=BH+CH=4+9=13(cm)

Xét ΔHAB vuông tại H và ΔACB vuông tại A có

\(\widehat{HBA}\) chung

Do đó: ΔHAB~ΔACB

=>\(\dfrac{BH}{BA}=\dfrac{BA}{BC}\)

=>\(BA^2=BH\cdot BC=4\cdot13=52\)

=>\(BA=\sqrt{52}=2\sqrt{13}\left(cm\right)\)

ΔABC vuông tại A

=>\(AB^2+AC^2=BC^2\)

=>\(AC^2=13^2-\left(2\sqrt{13}\right)^2=117\)

=>\(AC=\sqrt{117}=3\sqrt{13}\left(cm\right)\)

2: ΔHAB~ΔACB

=>\(\dfrac{HA}{AC}=\dfrac{AB}{CB}\)

=>\(HA=\dfrac{AB\cdot AC}{BC}=\dfrac{2\sqrt{13}\cdot3\sqrt{13}}{13}=6\left(cm\right)\)

Xét tứ giác AKHE có \(\widehat{AKH}=\widehat{AEH}=\widehat{KAE}=90^0\)

nên AKHE là hình chữ nhật

=>AH=KE

=>KE=6(cm)

3: Xét ΔAKH vuông tại K và ΔAHB vuông tại H có

\(\widehat{HAB}\) chung

Do đó: ΔAKH~ΔAHB

=>\(\dfrac{AK}{AH}=\dfrac{AH}{AB}\)

=>\(AH^2=AK\cdot AB\left(1\right)\)

Xét ΔAEH vuông tại E và ΔAHC vuông tại H có

\(\widehat{EAH}\) chung

Do đó: ΔAEH~ΔAHC

=>\(\dfrac{AE}{AH}=\dfrac{AH}{AC}\)

=>\(AH^2=AE\cdot AC\left(2\right)\)

Từ (1),(2) suy ra \(AK\cdot AB=AE\cdot AC\)

=>\(\dfrac{AK}{AC}=\dfrac{AE}{AB}\)

Xét ΔAKE vuông tại A và ΔACB vuông tại A có

\(\dfrac{AK}{AC}=\dfrac{AE}{AB}\)

Do đó: ΔAKE~ΔACB

4: ta có: ΔABC vuông tại A

mà AI là đường trung tuyến

nên IA=IC

=>ΔIAC cân tại I

=>\(\widehat{IAC}=\widehat{ICA}\)

ΔAKE~ΔACB

=>\(\widehat{AEK}=\widehat{ABC}\)

Ta có: \(\widehat{AEK}+\widehat{IAC}=\widehat{ABC}+\widehat{ACB}=90^0\)

=>EK\(\perp\)AI tại N

1. Tính AB, AC:

• Áp dụng định lý Pitago trong tam giác vuông AHB:
  • AB² = AH² + HB²
  • AH² = AB² - HB²
• Áp dụng định lý Pitago trong tam giác vuông AHC:
  • AC² = AH² + HC²
  • AH² = AC² - HC²
• Từ hai phương trình trên, ta có: AB² - HB² = AC² - HC²
• Suy ra: AB² = AC² - HC² + HB²
• Thay số: AB² = AC² - 9² + 4² = AC² - 65
• Áp dụng định lý Pitago trong tam giác vuông ABC:
  • BC² = AB² + AC²
  • BC² = (AC² - 65) + AC² = 2AC² - 65
• Thay BC = HB + HC = 4 + 9 = 13
  • 13² = 2AC² - 65
  • 2AC² = 13² + 65 = 224
  • AC² = 112
  • AC = √112 = 4√7 cm
• Thay AC vào phương trình AB² = AC² - 65:
  • AB² = (4√7)² - 65 = 112 - 65 = 47
  • AB = √47 cm

2. Tính KE:

• Áp dụng định lý Pitago trong tam giác vuông AKE:
  • KE² = AK² + AE²
• Áp dụng định lý Pitago trong tam giác vuông AHB:
  • AK² = AH² - HK²
• Áp dụng định lý Pitago trong tam giác vuông AHC:
  • AE² = AH² - HE²
• Thay vào phương trình KE²:
  • KE² = (AH² - HK²) + (AH² - HE²) = 2AH² - (HK² + HE²)
• Ta có: HK + HE = BC = 13 cm
• Áp dụng định lý Pitago trong tam giác vuông HKE:
  • KE² = HK² + HE² = (HK + HE)² - 2HK.HE = 13² - 2HK.HE
• Suy ra: 2AH² - (HK² + HE²) = 13² - 2HK.HE
• 2AH² = 13² + 2HK.HE
• AH² = (13² + 2HK.HE) / 2
• Thay AH² = AB² - HB²:
  • AB² - HB² = (13² + 2HK.HE) / 2
  • 2(AB² - HB²) = 13² + 2HK.HE
  • 2HK.HE = 2(AB² - HB²) - 13²
  • HK.HE = (AB² - HB²) - 13²/2
  • HK.HE = (47 - 4²) - 13²/2 = -65/2
• Vì HK và HE đều dương nên HK.HE = -65/2 là vô lý.
• Vậy, không thể tính KE bằng cách này.

3. Chứng minh AB.AK = AE.AC; AKE ~ ACB:

• Chứng minh AB.AK = AE.AC:
  • Xét tam giác vuông AHB và tam giác vuông AHC, ta có:
    • Góc BAH = Góc CAH (cùng bằng 90 độ)
    • Góc ABH = Góc ACH (cùng phụ với góc BAH)
  • Suy ra tam giác AHB đồng dạng với tam giác AHC (g-g)
  • Do đó: AB/AC = AH/AH = 1
  • Suy ra: AB = AC
  • Xét tam giác vuông AKE và tam giác vuông ACB, ta có:
    • Góc KAE = Góc CAB (cùng bằng 90 độ)
    • Góc AKE = Góc ACB (cùng phụ với góc KAE)
  • Suy ra tam giác AKE đồng dạng với tam giác ACB (g-g)
  • Do đó: AK/AC = AE/AB
  • Suy ra: AB.AK = AE.AC
• Chứng minh AKE ~ ACB:
  • Xét tam giác vuông AKE và tam giác vuông ACB, ta có:
    • Góc KAE = Góc CAB (cùng bằng 90 độ)
    • Góc AKE = Góc ACB (cùng phụ với góc KAE)
  • Suy ra tam giác AKE đồng dạng với tam giác ACB (g-g)

4. Chứng minh AI vuông góc KE tại N:

• Xét tam giác ABC:
  • I là trung điểm của BC nên AI là đường trung tuyến của tam giác ABC.
• Xét tam giác AKE:
  • N là giao điểm của AI và KE nên N là trọng tâm của tam giác AKE.
• Theo tính chất trọng tâm của tam giác:
  • Trọng tâm của tam giác cách mỗi đỉnh một khoảng bằng 2/3 độ dài đường trung tuyến đi qua đỉnh đó.
  • Do đó: AN = 2/3 AI
• Xét tam giác vuông AHI:
  • AI là đường trung tuyến của tam giác vuông AHI nên AI = 1/2 HI.
• Suy ra:
  • AN = 2/3 AI = 2/3 * (1/2 HI) = 1/3 HI
  • Do đó: IN = AI - AN = 1/2 HI - 1/3 HI = 1/6 HI
• Xét tam giác vuông HKE:
  • N là trung điểm của KE nên HN là đường trung tuyến của tam giác vuông HKE.
• Theo tính chất đường trung tuyến của tam giác vuông:
  • Đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền.
  • Do đó: HN = 1/2 KE
• Suy ra:
  • IN = 1/6 HI = 1/2 HN
  • Do đó: HN = 3IN
• Xét tam giác HIN:
  • HN = 3IN nên tam giác HIN vuông tại I (định lý đảo của định lý Pytago).
• Kết luận:
  • AI vuông góc KE tại N.

Lưu ý:

• Trong bài toán này, không thể tính KE bằng cách sử dụng định lý Pitago trong tam giác vuông HKE vì HK.HE là một số âm.
• Việc chứng minh AB.AK = AE.AC và AKE ~ ACB là cần thiết để chứng minh AI vuông góc KE tại N.
• Việc chứng minh AI vuông góc KE tại N là một ứng dụng của tính chất trọng tâm của tam giác và tính chất đường trung tuyến của tam giác vuông.
•  

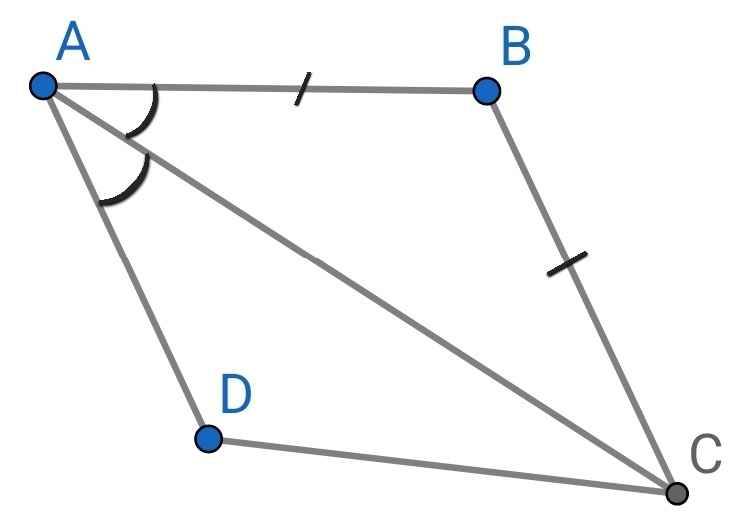
∆ABC có:

AB = BC (gt)

⇒ ∆ABC cân tại B

⇒ ∠BAC = ∠BCA (1)

Do AC là tia phân giác của ∠BAD (gt)

⇒ ∠DAC = ∠BAC (2)

Từ (1) và (2) ⇒ ∠BCA = ∠DAC

Mà ∠BCA và ∠DAC là hai góc so le trong

⇒ BC // AD

⇒ ABCD là hình thang

1. Chứng minh hợp kim tan hết:

• Xét phản ứng của Fe với H2SO4:
  • Fe + H2SO4 → FeSO4 + H2
  • n(Fe) = m(Fe) / M(Fe)
  • n(H2SO4) = C(H2SO4) * V(H2SO4) = 0,2 mol
  • Từ phương trình phản ứng, ta thấy n(Fe) = n(H2SO4) = 0,2 mol
  • m(Fe) = n(Fe) * M(Fe) = 11,2 gam
• Xét phản ứng của Ni với H2SO4:
  • Ni + H2SO4 → NiSO4 + H2
  • n(Ni) = m(Ni) / M(Ni) = (36,2 - 11,2) / 58,7 = 0,42 mol
  • n(H2SO4) = 0,2 mol
  • Từ phương trình phản ứng, ta thấy n(Ni) > n(H2SO4)
• Kết luận:
  • Hợp kim tan hết vì lượng H2SO4 đủ để phản ứng với cả Fe và Ni.

2. Hợp kim gấp đôi có tan hết hay không?

• Lượng Fe và Ni gấp đôi:
  • m(Fe) = 2 * 11,2 = 22,4 gam
  • m(Ni) = 2 * (36,2 - 11,2) = 50 gam
• Lượng H2SO4 không đổi:
  • n(H2SO4) = 0,2 mol
• Xét phản ứng:
  • n(Fe) = m(Fe) / M(Fe) = 0,4 mol
  • n(Ni) = m(Ni) / M(Ni) = 0,86 mol
  • Từ phương trình phản ứng, ta thấy n(Fe) + n(Ni) > n(H2SO4)
• Kết luận:
  • Hợp kim gấp đôi sẽ không tan hết vì lượng H2SO4 không đủ để phản ứng với cả Fe và Ni.

3. Tính khối lượng kim loại trong hợp kim:

• Tính lượng H2 sinh ra:
  • n(H2) = m(CuO) / M(CuO) = 48 / 80 = 0,6 mol
• Tính lượng Fe và Ni:
  • n(Fe) = n(H2) = 0,6 mol
  • n(Ni) = n(H2) - n(Fe) = 0,6 - 0,6 = 0 mol
• Tính khối lượng Fe và Ni:
  • m(Fe) = n(Fe) * M(Fe) = 0,6 * 56 = 33,6 gam
  • m(Ni) = n(Ni) * M(Ni) = 0 * 58,7 = 0 gam
• Kết luận:
  • Khối lượng Fe trong hợp kim là 33,6 gam.
  • Khối lượng Ni trong hợp kim là 0 gam.

Lưu ý:

• Trong bài toán này, ta giả định rằng phản ứng xảy ra hoàn toàn.
• Nồng độ của dung dịch H2SO4 là 0,2M, không phải 0,耀M như trong đề bài.

Hy vọng bài giải này giúp bạn hiểu rõ hơn về bài toán.

a: Xét ΔAEF có

AH là đường cao

AH là đường phân giác

Do đó: ΔAEF cân tại A

Xét ΔAEF có BM//EF

nên \(\dfrac{AB}{AE}=\dfrac{AM}{AF}\)

mà AE=AF

nên AB=AM

=>ΔABM cân tại A

b: Kẻ BK//AC(K\(\in\)EF)

Xét tứ giác BMFK có

BM//FK

BK//MF

DO đó: BMFK là hình bình hành

=>BK=MF

Xét ΔBDK và ΔCDF có

\(\widehat{BDK}=\widehat{CDF}\)(hai góc đối đỉnh)

DB=DC

\(\widehat{DBK}=\widehat{DCF}\)(BK//CF)

Do đó: ΔBDK=ΔCDF

=>BK=CF

Ta có: BK//FC

=>\(\widehat{BKE}=\widehat{AFE}\)

=>\(\widehat{BKE}=\widehat{BEK}\)

=>BE=BK

mà BK=FC và BK=MF

nên MF=BE=CF

\(\left(2x-3\right)^2-\left(x-5\right)\left(4x^2-1\right)=7x+6\)

=>\(4x^2-12x+9-\left(4x^3-x-20x^2+5\right)=7x+6\)

=>\(4x^2-12x+9-4x^3+20x^2+x-5-7x-6=0\)

=>\(-4x^3+24x^2-18x-2=0\)

=>\(-4x^3+4x^2+20x^2-20x+2x-2=0\)

=>\(-4x^2\left(x-1\right)+20x\left(x-1\right)+2\left(x-1\right)=0\)

=>\(\left(x-1\right)\left(-4x^2+20x+2\right)=0\)

=>\(\left[{}\begin{matrix}x-1=0\\-4x^2+20x+2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=\dfrac{5\pm3\sqrt{3}}{2}\end{matrix}\right.\)

mong các bạn giúp đỡ 

ngày 12/6 là mình đi học rồi vào buổi sáng

Help tui vs mn <:_((

Biện pháp tu từ nhân hóa nhé.

\(\frac{x-1}{1999}+\frac{x-2}{1998}=\frac{x-3}{1997}+\frac{x-4}{1996}\\\Leftrightarrow \left(\frac{x-1}{1999}-1\right) +\left(\frac{x-2}{1998}-1\right)=\left(\frac{x-3}{1997}-1\right)+\left(\frac{x-4}{1996}-1\right)\\\Leftrightarrow \frac{x-2000}{1999}+\frac{x-2000}{1998}=\frac{x-2000}{1997}+\frac{x-2000}{1996}\\\Leftrightarrow \frac{x-2000}{1999}+\frac{x-2000}{1998}-\frac{x-2000}{1997}-\frac{x-2000}{1996}=0\\ \Leftrightarrow (x-2000)\left(\frac{1}{1999}+\frac{1}{1998}-\frac{1}{1997}-\frac{1}{1996}\right)=0\\\Leftrightarrow x-2000=0\left(\text{vì } \frac{1}{1999}+\frac{1}{1998}-\frac{1}{1997}-\frac{1}{1996}\ne0\right)\\\Leftrightarrow x=2000\)

Vậy phương trình đã cho có 1 nghiệm duy nhất là \(x=2000\).

cứu tui với ăng em