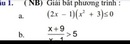\(a,f\left(x\right)=\frac{x}{\sqrt{4-x}}\)

\(ĐKXĐ:4-x>0< =>x< 4\)

\(TXĐ:D=\left(4;-\infty\right)\)

ta có \(-5\in D\)nhưng \(5\notin D\)

hs ko chẵn cũng ko lẻ

\(b,f\left(x\right)=\sqrt{2x-1}+\sqrt{1+2x}\)

\(ĐKXĐ:x\ge\frac{1}{2};x\ge-\frac{1}{2}< =>x\ge\frac{1}{2}\)

\(TXĐ:D=[\frac{1}{2};+\infty)\)

bạn biện luận như câu trên thì ra đc hàm số ko chẵn cũng ko lẻ

\(c,f\left(x\right)=\sqrt{x-2}+\frac{1}{2+x}\)

\(ĐKXĐ:x\ge2;x\ne-2< =>x\ge2\)

\(D=[2;+\infty)\)

ta có \(3\in D\)nhưng \(-3\notin D\)nên hàm số ko chẵn cũng ko lẻ

\(d,f\left(x\right)=\left|2x-3\right|-\left|2x+3\right|\)

\(TXĐ:D=|R\)

\(\forall x\in D< =>-x\in D\)

\(-f\left(x\right)=\left|-2x-3\right|-\left|-2x+3\right|\)

\(-f\left(x\right)=\left|-\left(2x+3\right)\right|-\left|-\left(2x-3\right)\right|\)

\(-f\left(x\right)=\left|2x+3\right|-\left|2x-3\right|\)

\(-f\left(x\right)=-\left(-\left|2x+3\right|+\left|2x-3\right|\right)\)

\(-f\left(x\right)=-\left(\left|2x-3\right|-\left|2x+3\right|\right)=f\left(-x\right)\)

hàm số lẻ

hai câu còn lại cậu làm nốt hen

Sự khác nhau giữa doanh nghiệp nhỏ và kinh doanh hộ gia đình

- Doanh nghiệp nhỏ: DN nhỏ có tư cách pháp nhân, theo đó các thành viên chịu trách nhiệm hữu hạn, tức là chỉ chịu trách nhiệm trong phạm vi phần vốn góp vào doanh nghiệp. - Hộ kinh doanh gia đình: Hộ kinh doanh gia đình không có tư cách pháp nhân tức là hộ kinh doanh phải chịu trách nhiệm vô hạn bằng tài sản của mình.

Ta có: \(a,b\)không chia hết cho \(3\)do đó \(a^2\equiv1\left(mod3\right),b^2\equiv1\left(mod3\right)\).

\(a^2-b^2=\left(a^2-1\right)-\left(b^2-1\right)\).

Ta sẽ chứng minh \(a^2-1⋮24\).

\(24=3.8,\left(3,8\right)=1\)do đó ta sẽ chứng minh \(a^2-1\)chia hết cho \(3\)và \(8\).

- \(a^2-1⋮3\)chứng minh trên. 

\(a^2-1=\left(a-1\right)\left(a+1\right)\)là tích của hai số chẵn liên tiếp nên có một thừa số chia hết cho \(2\)(nhưng không chia hết cho \(4\)), một thừa số chia hết cho \(4\)do đó chia hết cho \(2.4=8\).

Tương tự với \(b^2-1\).

Do đó ta có đpcm. 

\(\hept{\begin{cases}x+m\le0\\-x+5< 0\end{cases}\hept{\begin{cases}x\le-m\\x< -5\end{cases}\hept{\begin{cases}x\in\left(-\infty;-m\right)\\x\in\left(-\infty;-5\right)\end{cases}}}}\)bạn sửa lại chỗ trên nha là nửa khoảng

\(+-m\ge-5\)

\(m\le5< =>\)tập nghiệm của HPT \(S=\left(-m;-\infty\right)\)

\(+-m< 5\)

\(m>5< =>\)tập nghiệm của HPT \(S=\left\{-\infty;-5\right\}\)

a. ta có \(x^2+3>0\text{ nên }\left(2x-1\right)\left(x^2+1\right)\le0\Leftrightarrow2x-1\le0\Leftrightarrow x\le\frac{1}{2}\)

b. ta có \(\frac{x+9}{x-1}>5\Leftrightarrow\frac{x+9-5x+5}{x-1}>0\Leftrightarrow\frac{14-4x}{x-1}>0\)

\(\hept{\begin{cases}14-4x>0\\x-1>0\end{cases}\Leftrightarrow\frac{7}{2}>x>1}\) hoặc \(\hept{\begin{cases}14-4x< 0\\x-1< 0\end{cases}\Leftrightarrow\hept{\begin{cases}x>\frac{7}{2}\\x< 1\end{cases}}}\) vô lí

vậy \(1< x< \frac{7}{2}\)

a) \(\left(2x-1\right)\left(x^2+3\right)\le0\)

\(\Leftrightarrow\hept{\begin{cases}2x-1\le0\\x^2+3\ge0\end{cases}}\)hoặc \(\hept{\begin{cases}2x-1\ge0\\x^2+3\le0\end{cases}}\)

mà \(x^2+3>0\forall x\)

nên \(\hept{\begin{cases}2x-1\le0\\x^2+3>0\end{cases}}\)

\(\Leftrightarrow x\le\frac{1}{2}\)

Vậy nghiệm của BPT là \(x\le\frac{1}{2}\)

b) Đề bị che mất mẫu số nên không đọc được đề =))