Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Để \(\dfrac{\sqrt{n}-1}{2}\inℤ\) thì \(\sqrt{n}-1⋮2\) \(\Rightarrow\) \(n\) là số chính phương lẻ.
Mà \(n< 82\) nên \(n\in\left\{1,9,25,49,81\right\}\)
Vậy \(n\in\left\{1,9,25,49,81\right\}\) thỏa mãn ycbt.

(9².2¹⁴)/(8².6⁷)
= [(3²)².2¹⁴]/[(2³)².2⁷.3⁷]
= (3⁴.2¹⁴)/(2⁶.2⁷.3⁷)
= 2¹⁴/(2¹³.3³)
= 2/3³
= 2/27

`#3107.101107`
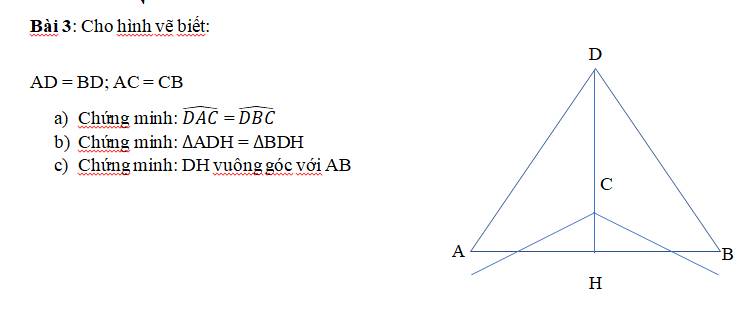
`a,`
Xét $\triangle ABH$ và $\triangle ACH$:
`AB = AC` $(\triangle ABC$cân tại A`)`
\(\widehat{B}=\widehat{C}\) $(\triangle ABC$cân tại A`)`
`HB = HC ( H` là trung điểm của BC`)`
$=> \triangle ABH = \triangle ACH (c - g - c)$
Vì $\triangle ABH = \triangle ACH$
`=>`\(\widehat{AHB}=\widehat{AHC}\left(\text{2 góc tương ứng}\right)\)
Mà `2` góc này nằm ở vị trí kề bù
`=>` \(\widehat{AHB}+\widehat{AHC}=180^0\)
`=>` \(\widehat{AHB}=\widehat{AHC}=\dfrac{180^0}{2}=90^0\) `=> AH \bot BC`
`b,`
Vì $\triangle ABH = \triangle ACH (a)$
`=>`\(\widehat{BAH}=\widehat{CAH}\left(\text{2 góc tương ứng}\right)\)
Xét $\triangle AHM$ và $\triangle AHN$:
AH chung
\(\widehat{MAH}=\widehat{NAH}\left(CMT\right)\)
\(\widehat{AMH}=\widehat{ANH}\left(=90^0\right)\)
$=> \triangle AHM = \triangle AHN (ch - gn)$
`c,`
Xét $\triangle HMB$ và $\triangle HNC$:
\(\widehat{HMB}=\widehat{HNC}\left(=90^0\right)\)
`HB = HC` `(`gt`)`
\(\widehat{HBM}=\widehat{HCN}\) $(\triangle ABC$ cân tại A`)`
$=> \triangle HMB = \triangle HNC (ch - gn)$
`=>`\(\widehat{BHM}=\widehat{CHN}\left(2\text{ góc tương ứng}\right)\) `(1)`
Vì \(\left\{{}\begin{matrix}\widehat{MHB}+\widehat{KHB}=\widehat{MHK}\\\widehat{NHC}+\widehat{IHC}=\widehat{NHI}\end{matrix}\right.\)
Mà \(\widehat{MHK}=\widehat{NHI}\left(\text{đối đỉnh}\right)\) `(2)`
Từ `(1)` và `(2)` `=>` \(\widehat{KHB}=\widehat{IHC}\)
Xét $\triangle KHB$ và $\triangle IHC$:
\(\widehat{KBH}=\widehat{ICH}\left(\widehat{ABC}=\widehat{ACB}\right)\)
`HB = HC`
\(\widehat{KHB}=\widehat{IHC}\)
$=> \triangle KHB = \triangle IHC (g - c - g)$
`=> BK = CI` `(2` cạnh tương ứng`)`
Ta có:
`AK = AB + BK`
`AI = AC + CI`
Mà `AB = AC; BK = CI`
$=> AK = AI => \triangle AIK$ cân tại A.

Gọi x, y, z là ba số cần tìm
Do x, y, z tỉ lệ thuận với 3; 4; 5 nên:
x/3 = y/4 = c/5
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
x/3 = y/4 = c/5 = (a + b + c)/(3 + 4 + 5) = 552/12 = 46
x/3 = 46 ⇒ x = 46.3 = 138
y/4 = 46 ⇒ y = 46.4 = 184
z/5 = 46 ⇒ z = 46.5 = 230
Vậy ba số cần tìm là 138; 184; 230
cho 30 đường thẳng phân biệt đi qua tâm O . hỏi có bao nhiêu cặp góc đối đỉnh ( không tính góc bẹt )


Bài 10
Do a và b tỉ lệ thuận với 7 và 9
⇒ a/7 = b/9
⇒ 3a/21 = 2b/18
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
3a/21 = 2b/18 = (3a - 2b)/(21 - 18) 30/3 = 10
3a/21 = 10 ⇒ a = 10.21:3 = 70
2b/18 = 10 ⇒ b = 10.18:2 = 90
Vậy a = 70; b = 90
Bài 9
Do x và y tỉ lệ thuận với 3 và 5
⇒ x/3 = y/5
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
x/3 = y/5 = (x + y)/(3 + 5) = 24/8 = 3
x/3 = 3 ⇒ x = 3.3 = 9
y/5 = 3 ⇒ y = 5.3 = 15
Vậy x = 9; y = 15

Lời giải:
Vì $|y|\geq 0$ với mọi $y$ nên:
$(x+3)(1-x)=|y|\geq 0$. Khi đó sẽ có 2 TH xảy ra:
TH1: $x+3\geq 0; 1-x\geq 0$
$\Rightarrow 1\geq x\geq -3$
Mà $x$ nguyên nên $x\in \left\{1; 0; -1; -2; -3\right\}$
Nếu $x=1$ thì: $|y|=0\Rightarrow y=0$
Nếu $x=0$ thì $|y|=3\Rightarrow y=\pm 3$
Nếu $x=-1$ thì $|y|=4\Rightarrow y=\pm 4$
Nếu $x=-2$ thì $|y|=3\Rightarrow y=\pm 3$
Nếu $x=-3$ thì $|y|=0\Rightarrow y=0$
TH2: $x+3\leq 0; 1-x\leq 0\Rightarrow x\geq 1$ và $x\leq -3$ (vô lý) - loại.
