sao lại \(2x^x\)

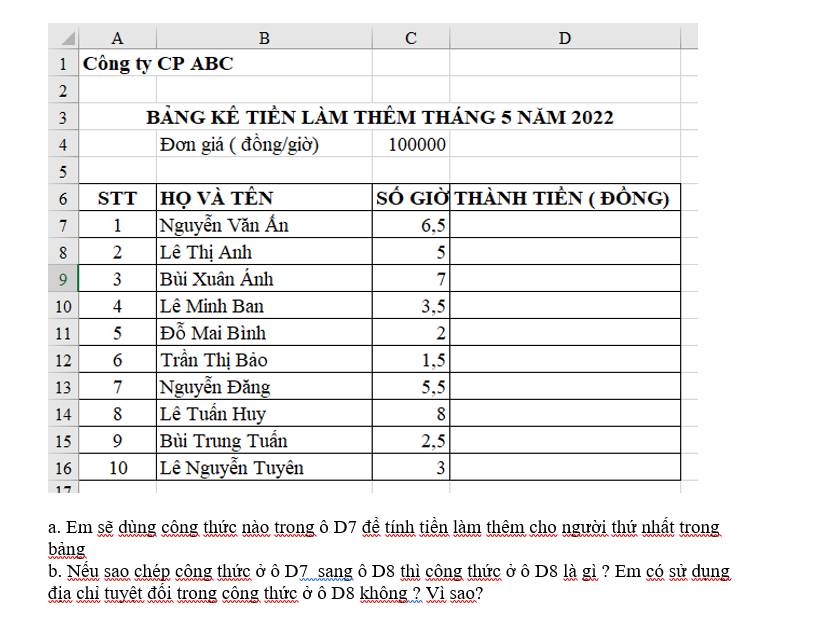
a,Công thức là:   =D7*C4

b,Ko.Vì nếu dùng địa chỉ tuyệt đối thì công thức vẫn tự động chạy xuống theo khi mà ta copy công thức xuông ô D8

25x²y² . 1/5 xy

= (25 . 1/5).(x².x)(.(y².y)

= 5.x³y³

\(25x^2y^2.\dfrac{1}{5}xy\)

\(=\left(25.\dfrac{1}{5}\right).\left(x^2.x\right).\left(y^2.y\right)\)

\(=5.\left(x^{2+1}\right).\left(y^{2+1}\right)\)

\(=5.x^3.y^3\)

a) \(\Delta ABC\) cân tại A, có AM là đường trung tuyến

\(\Rightarrow AM\) cũng là đường trung trực của \(\Delta ABC\)

\(\Rightarrow AM\perp BC\)

\(\Rightarrow\widehat{AMC}=90^0\)

Tứ giác \(AMCN\) có:

\(I\) là trung điểm của AC (gt)

\(I\) là trung điểm của MN (gt)

\(\Rightarrow AMCN\) là hình bình hành

Mà \(\widehat{AMC}=90^0\)

\(\Rightarrow AMCN\) là hình chữ nhật

b) Do \(AMCN\) là hình chữ nhật

\(\Rightarrow AN=CM\) và \(AN\) // \(CM\)

Do \(AN\) // \(CM\) (cmt)

\(\Rightarrow AN\) // \(BM\)

Do \(M\) là trung điểm của \(BC\) (gt)

\(\Rightarrow BM=CM\)

Mà \(AN=CM\left(cmt\right)\)

\(\Rightarrow BM=AN\)

Tứ giác \(ABMN\) có:

\(BM\) // \(AN\) (cmt)

\(BM=AN\left(cmt\right)\)

\(\Rightarrow ABMN\) là hình bình hành

Mà \(E\) là trung điểm của AM

\(\Rightarrow E\) là trung điểm của BN

a

14cm

14cm

giúp câu 10 vs ạ các câu khác không cần đâu ạ