Gọi số cần tìm có dạng là \(\overline{ab}\)

Chữ số hàng đơn vị gấp 2 lần chữ số hàng chục nên b=2a

Nếu thêm chữ số 1 vào giữa hai chữ số ấy thì được số mới lớn hơn số ban đầu là 370 nên \(\overline{a1b}-\overline{ab}=370\)

=>100a+10+b-10a-b=370

=>90a=360

=>a=4

=>\(b=2\cdot4=8\)

Vậy: Số cần tìm là 48

Gọi chữ số hàng chục là $x$ ($x\in\mathbb{N}^*$)

Chữ số hàng đơn vị là: $2x$

Khi đó số cần tìm là: $\overline{x(2x)}$

Vì nếu thêm chữ số 1 xen giữa hai chữ số ấy thì được số mới lớn hơn số ban đầu là 370 nên ta có phương trình:

$\overline{x1(2x)}-\overline{x(2x)}=370$

$\Leftrightarrow (100x+10+2x)-(10x+2x)=370$

$\Leftrightarrow 102x+10-12x=370$

$\Leftrightarrow 90x=360$

$\Leftrightarrow x=4$ (tmdk)

Khi đó, chữ số hàng đơn vị là: $2\times4=8$

Vậy số cần tìm là 48.

#$\mathtt{Toru}$

Điều kiện xác định: \(a;b\ge0\)

Nhận xét:

\(2\sqrt{ab}\ge0\\ \Leftrightarrow a+b\le a+2\sqrt{ab}+b\\ \Leftrightarrow\left(\sqrt{a+b}\right)^2\le\left(\sqrt{a}+\sqrt{b}\right)^2\\ \Leftrightarrow\sqrt{a+b}\le\sqrt{a}+\sqrt{b}\)

Vậy...

Đề đọc khó hiểu quá. Bạn nên viết đề bằng công thức toán (biểu tượng $\sum$ góc trái khung soạn thảo) để mọi người hiểu đề của bạn hơn nhé.

a: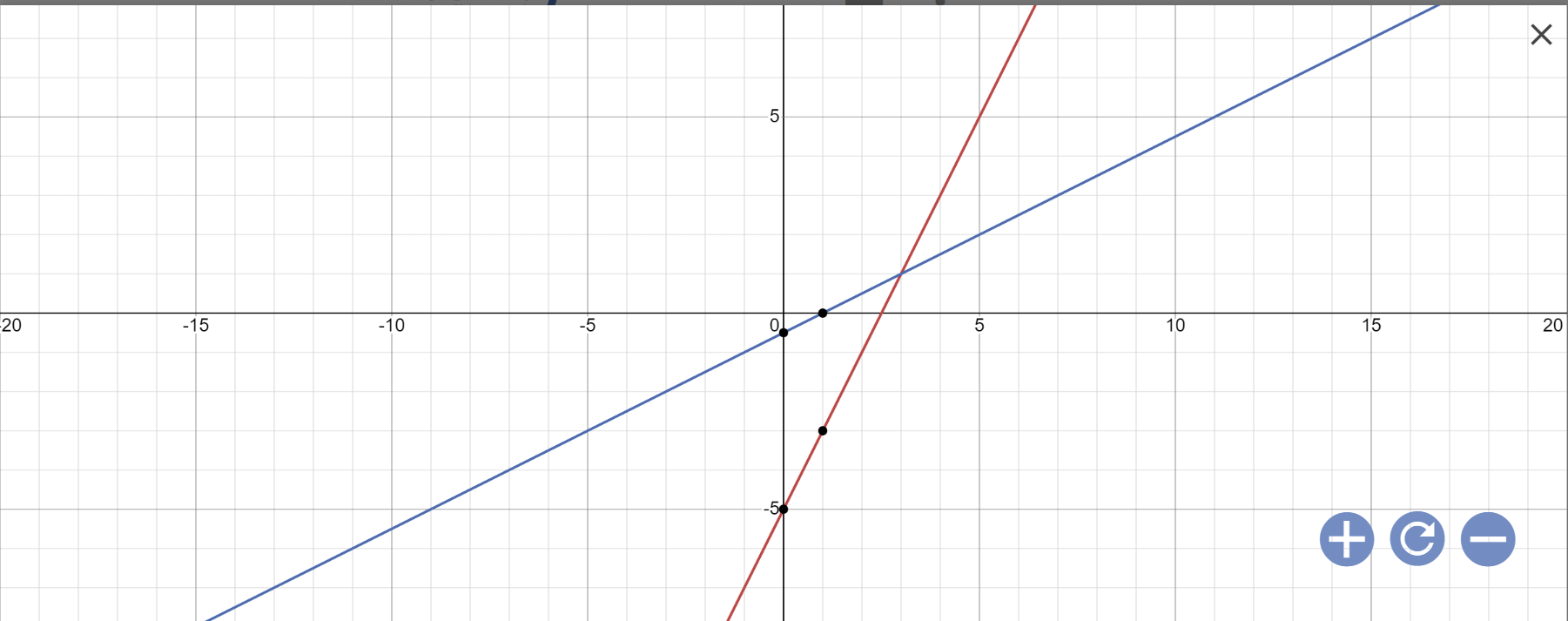 

b: Nghiệm của hệ phương trình\(\left\{{}\begin{matrix}2x-y=5\\x-2y=1\end{matrix}\right.\) chính là giao điểm của (d1),(d2)

Theo đồ thị, ta thấy (d1) cắt (d2) tại A(3;1)

=>Nghiệm của hệ phương trình \(\left\{{}\begin{matrix}2x-y=5\\x-2y=1\end{matrix}\right.\) là \(\left\{{}\begin{matrix}x=3\\y=1\end{matrix}\right.\)

c: Thay x=3 và y=1 vào (d3), ta được:

\(3m+\left(2m-1\right)\cdot1=3\)

=>5m-1=3

=>5m=4

=>\(m=\dfrac{4}{5}\)

\(\left(x^2-4\right)+\left(x-2\right)\left(3-2x\right)=0\\ \Leftrightarrow\left(x-2\right)\left(x+2\right)+\left(x-2\right)\left(3-2x\right)=0\\ \Leftrightarrow\left(x-2\right)\left(x+2+3-2x\right)=0\\ \Leftrightarrow\left(x-2\right)\left(5-x\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x-2=0\\5-x=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=2\\x=5\end{matrix}\right.\)

\(\left(2x-3\right)\left(5x+1\right)=\left(3-2x\right)\left(x-5\right)\)

=>\(\left(2x-3\right)\left(5x+1\right)-\left(3-2x\right)\left(x-5\right)=0\)

=>\(\left(2x-3\right)\left(5x+1\right)+\left(2x-3\right)\left(x-5\right)=0\)

=>\(\left(2x-3\right)\left(5x+1+x-5\right)=0\)

=>\(\left(2x-3\right)\left(6x-4\right)=0\)

=>\(2\left(2x-3\right)\left(3x-2\right)=0\)

=>(2x-3)(3x-2)=0

=>\(\left[{}\begin{matrix}2x-3=0\\3x-2=0\end{matrix}\right.\)

=>\(\left[{}\begin{matrix}x=\dfrac{3}{2}\\x=\dfrac{2}{3}\end{matrix}\right.\)

\(\left(2x-3\right)\left(5x+1\right)=\left(3-2x\right)\left(x-5\right)\\ \Leftrightarrow\left(2x-3\right)\left(5x+1\right)+\left(2x-3\right)\left(x-5\right)=0\\ \Leftrightarrow\left(2x-3\right)\left(5x+1+x-5\right)=0\\ \Leftrightarrow\left(2x-3\right)\left(6x-4\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}2x-3=0\\6x-4=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=3\\6x=4\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\\x=\dfrac{2}{3}\end{matrix}\right.\)

\(\left(x-1\right)\left(x+7\right)=\left(1-x\right)\left(3-2x\right)\)

=>\(\left(x+7\right)\left(x-1\right)=\left(x-1\right)\left(2x-3\right)\)

=>\(\left(2x-3\right)\left(x-1\right)-\left(x-1\right)\left(x+7\right)=0\)

=>\(\left(x-1\right)\left(2x-3-x-7\right)=0\)

=>(x-1)(x-10)=0

=>\(\left[{}\begin{matrix}x=1\\x=10\end{matrix}\right.\)

\(\left(x-1\right)\left(x+7\right)=\left(1-x\right)\left(3-2x\right)\\ \Leftrightarrow\left(x-1\right)\left(x+7\right)+\left(x-1\right)\left(3-2x\right)=0\\ \Leftrightarrow\left(x-1\right)\left(x+7+3-2x\right)=0\\ \Leftrightarrow\left(x-1\right)\left(10-x\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x-1=0\\10-x=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=1\\x=10\end{matrix}\right.\)

\(-5\left(4x-1\right)\left(x-2\right)=2\left(4x-1\right)^2\\ \Leftrightarrow\left(4x-1\right)\left(-5x+10\right)-2\left(4x-1\right)^2=0\\ \Leftrightarrow\left(4x-1\right)\left(-5x+10-8x+2\right)=0\\ \Leftrightarrow\left(4x-1\right)\left(-13x+12\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}4x-1=0\\-13x+12=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}4x=1\\13x=12\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{4}\\x=\dfrac{12}{13}\end{matrix}\right.\)