
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


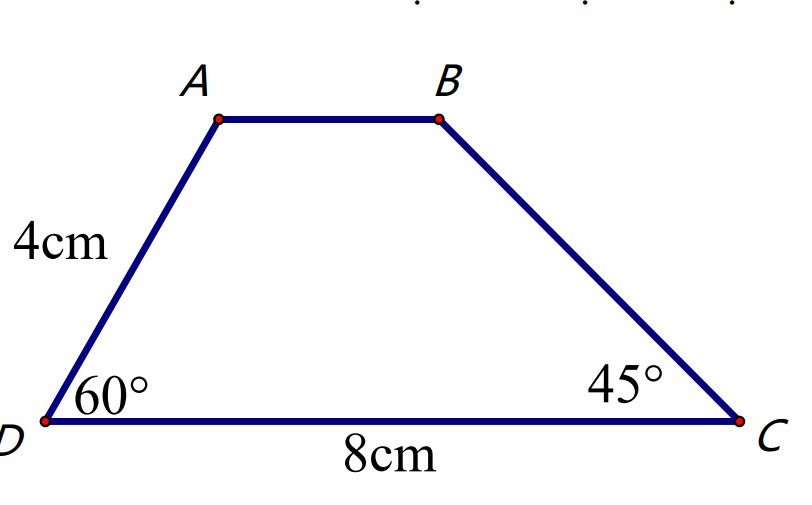
A B C D H K
Dựng \(AH\perp CD;BK\perp CD\left(H;K\in CD\right)\)
Xét tg vuông ADH có
\(\widehat{DAH}=90^o-\widehat{D}=30^o\)
\(\Rightarrow DH=\dfrac{AD}{2}=\dfrac{4}{2}=2cm\) (trong tg vuông cạnh đối diện góc \(30^o\) băng nửa cạnh huyền)
\(\Rightarrow AH=\sqrt{AD^2-DH^2}=\sqrt{16-4}=\sqrt{12}=2\sqrt{3}cm\)
\(\Rightarrow AH=BK=2\sqrt{3}cm\) (đường cao của hình thang)
Xét tg vuông BCK có
\(\widehat{KBC}=90^o-\widehat{C}=45^o\)
=> tg BCK vuông cân tại K \(\Rightarrow CK=BK=2\sqrt{3}cm\)
\(\Rightarrow BC=\sqrt{BK^2+CK^2}=\sqrt{12+12}=2\sqrt{6}cm\)
Xét HCN ABKH có
\(AB=KH=CD-DH-CK=8-2\sqrt{3}-2\sqrt{3}=8-4\sqrt{3}=4\left(2-\sqrt{3}\right)cm\)

a: \(\left(a+b\right)^3+\left(a-b\right)^3-2a^3\)
\(=a^3+3a^2b+3ab^2+b^3+a^3-3a^2b+3ab^2-b^3-2a^3\)
\(=6ab^2\)
b: \(\left(x-2\right)\left(x^2+2x+4\right)-\left(x+1\right)^3+3\left(x-1\right)\left(x+1\right)\)
\(=x^3-8-x^3-3x^2-3x-1+3\left(x^2-1\right)\)
\(=-3x^2-3x-9+3x^2-3=-3x-12\)

\(\left(x+3\right)\left(x^2-3x+9\right)=28\)
=>\(x^3+27=28\)
=>\(x^3=1=1^3\)
=>x=1

\(\dfrac{2020^3+1}{2020^2-2019}=\dfrac{\left(2020+1\right)\left(2020^2-2020\cdot1+1\right)}{2020^2-2019}\)
\(=\dfrac{2021\cdot\left(2020^2-2019\right)}{2020^2-2019}\)
=2021

Sửa đề: \(\dfrac{2020^3-1}{2020^2+2021}\)
\(=\dfrac{\left(2020-1\right)\left(2020^2+2020+1\right)}{2020^2+2020+1}\)
=2020-1=2019

ĐKXĐ: \(x\ne2\)
\(P=\dfrac{x^4-16}{x^4-4x^3+8x^2-16x+16}\)
\(=\dfrac{\left(x-2\right)\left(x+2\right)\left(x^2+4\right)}{x^4+4x^2-4x^3-16x+4x^2+16}\)
\(=\dfrac{\left(x-2\right)\left(x+2\right)\left(x^2+4\right)}{x^2\left(x^2+4\right)-4x\left(x^2+4\right)+4\left(x^2+4\right)}\)
\(=\dfrac{\left(x-2\right)\left(x+2\right)}{x^2-4x+4}=\dfrac{x+2}{x-2}\)
Để P nguyên thì \(x+2⋮x-2\)
=>\(x-2+4⋮x-2\)
=>\(4⋮x-2\)
=>\(x-2\in\left\{1;-1;2;-2;4;-4\right\}\)
=>\(x\in\left\{3;1;4;0;6;-2\right\}\)

a: \(P=27-27x+9x^2-x^3\)
\(=3^3-3\cdot3^2\cdot x+3\cdot3\cdot x^2-x^3=\left(3-x\right)^3\)
Khi x=-17 thì \(P=\left[3-\left(-17\right)\right]^3=\left(3+17\right)^3=20^3=8000\)
b: \(Q=x^3+3x^2+3x\)
\(=x^3+3x^2+3x+1-1\)
\(=\left(x+1\right)^3-1\)
Khi x=99 thì \(Q=\left(99+1\right)^3-1=100^3-1=1000000-1=999999\)

\(a.\left(x^2-2\right)^2=\left(x^2\right)^2-2\cdot x^2\cdot2+2^2=x^4-4x^2+4\\ b.\left(x+2y\right)^2=x^2+2\cdot x\cdot2y+\left(2y\right)^2=x^2+4xy+4y^2\\ c.\left(\dfrac{1}{2}-x\right)^2=\left(\dfrac{1}{2}\right)^2-2\cdot x\cdot\dfrac{1}{2}+x^2=\dfrac{1}{4}-x+x^2\\ d.\left(2a-1\right)^2=\left(2a\right)^2-2\cdot2a\cdot1+1^2=4a^2-4a+1\\ e.\left(\dfrac{1}{3}a+2\right)^2=\left(\dfrac{1}{3}a\right)^2+2\cdot\dfrac{1}{3}a\cdot2+2^2=\dfrac{1}{9}a^2+\dfrac{4}{3}a+4\\ f.\left(2a-\dfrac{2}{3}\right)^2=\left(2a\right)^2-2\cdot2a\cdot\dfrac{2}{3}+\left(\dfrac{2}{3}\right)^2=4a^2-\dfrac{8}{3}a+\dfrac{4}{9}\)

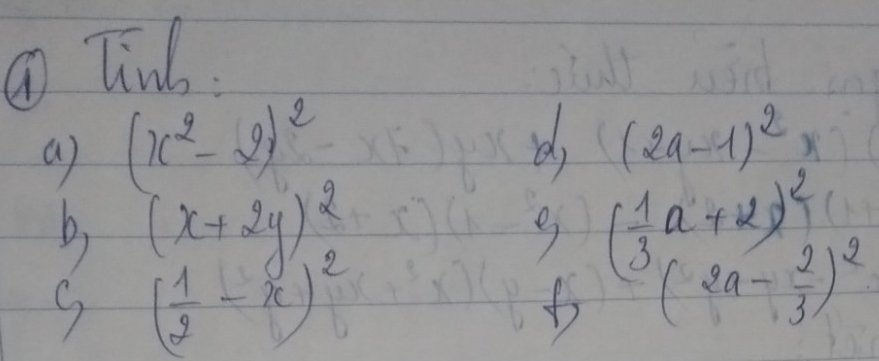
1: \(x^2-25=\left(x-5\right)\left(x+5\right)\)
2: \(9x^2-\dfrac{1}{16}y^2=\left(3x\right)^2-\left(\dfrac{1}{4}y\right)^2\)
\(=\left(3x-\dfrac{1}{4}y\right)\left(3x+\dfrac{1}{4}y\right)\)
3: \(x^6-y^4=\left(x^3\right)^2-\left(y^2\right)^2=\left(x^3-y^2\right)\left(x^3+y^2\right)\)
4: \(\left(2x-5\right)^2-64=\left(2x-5-8\right)\left(2x-5+8\right)\)
\(=\left(2x-13\right)\left(2x+3\right)\)
5: \(81-\left(3x+2\right)^2\)
\(=\left(9-3x-2\right)\left(9+3x+2\right)\)
\(=\left(-3x+7\right)\left(3x+11\right)\)
6: \(9\left(x-5y\right)^2-16\left(x+y\right)^2\)
\(=\left(3x-15y\right)^2-\left(4x+4y\right)^2\)
\(=\left(3x-15y-4x-4y\right)\left(3x-15y+4x+4y\right)\)
\(=\left(-x-19y\right)\left(7x-11y\right)\)
7: \(x^3-8=x^3-2^3=\left(x-2\right)\left(x^2+2x+4\right)\)
8: \(27x^3+125y^3=\left(3x\right)^3+\left(5y\right)^3\)
\(=\left(3x+5y\right)\left(9x^2-15xy+25y^2\right)\)
9: \(x^6+216=\left(x^2\right)^3+6^3\)
\(=\left(x^2+6\right)\left(x^4-6x^2+36\right)\)
10: \(x^2+8x+16=x^2+2\cdot x\cdot4+4^2=\left(x+4\right)^2\)
11: \(9x^2-12xy+4y^2\)
\(=\left(3x\right)^2-2\cdot3x\cdot2y+\left(2y\right)^2\)
\(=\left(3x-2y\right)^2\)
12: \(-25x^2y^2+10xy-1\)
\(=-\left[\left(5xy\right)^2-2\cdot5xy\cdot1+1^2\right]\)
\(=-\left(5xy-1\right)^2\)
13: \(x^3-6x^2+12x-8\)
\(=x^3-3\cdot x^2\cdot2+3\cdot x\cdot2^2-2^3\)
\(=\left(x-2\right)^3\)
14: \(8x^3+12x^2y+6xy^2+y^3\)
\(=\left(2x\right)^3+3\cdot\left(2x\right)^2\cdot y+3\cdot2x\cdot y^2+y^3\)
\(=\left(2x+y\right)^3\)