1 - 3/99.96 - 3/96.93 - 3/93.90 - ..... - 3/7.4 - 3/4
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


-4x+7y+13=0 chuyển thành 4x-7y=13
5x+3y=7 nhân hai vế với 4 ta có 20x+12y=28
3x-5y+4x-7y=13+1=14
7x-12y=14
20x+12y+7x-12y=42
27x=42
x=42/27 ( loại vì x là số nguyên )
vậy ko có x,y nào thoả mãn
(nếu mình sai thì cho mình xin lỗi nha)



\(\left(\dfrac{1}{16}\right)^x=\left(\dfrac{1}{32}\right)^{16}\\ =>\left[\left(\dfrac{1}{2}\right)^4\right]^x=\left[\left(\dfrac{1}{2}\right)^5\right]^{16}\\ =>\left(\dfrac{1}{2}\right)^{4\cdot x}=\left(\dfrac{1}{2}\right)^{5\cdot16}\\ =>\left(\dfrac{1}{2}\right)^{4x}=\left(\dfrac{1}{2}\right)^{80}\\ =>4x=80\\ =>x=\dfrac{80}{4}\\ =>x=20\)
Vậy: ..

Ta có:
+)
\(\dfrac{2023.2024-1}{2023.2024}\\ =\dfrac{2023.2024}{2023.2024}-\dfrac{1}{2023.2024}\\ =1-\dfrac{1}{2023.2024}\)
+)
\(\dfrac{2022.2023-1}{2022.2023}\\ =\dfrac{2022.2023}{2022.2023}-\dfrac{1}{2022.2023}\\ =1-\dfrac{1}{2022.2023}\)
Nhận xét:
Vì \(2023.2024>2022.2023\) nên:
\(\dfrac{1}{2023.2024}< \dfrac{1}{2022.2023}\\\Rightarrow1-\dfrac{1}{2023.2024}>1-\dfrac{1}{2022.2023}\)
hay \(\dfrac{2023.2024-1}{2023.2024}>\dfrac{2022.2023-1}{2022.2023}\)
Vậy...

\(2x\left(x-\dfrac{1}{7}\right)=0\)
\(2x=0\) hoặc \(x-\dfrac{1}{7}=0\)
\(x=0\) hoặc \(x=\dfrac{1}{7}\)

a.
Để A là phân số
\(\Rightarrow x+7\ne0\)
\(\Rightarrow x\ne7\)
b.
Để P nguyên \(\Rightarrow-\dfrac{3}{x+7}\) là số nguyên
\(\Rightarrow3\) chia hết `x+7`
\(\Rightarrow x+7\) là ước của 3
\(\Rightarrow x+7=\left\{-3;-1;1;3\right\}\)
\(\Rightarrow x=\left\{-10;-8;-6;-4\right\}\)
c.
\(P=-\dfrac{2}{3}\Rightarrow-\dfrac{3}{x+7}=-\dfrac{2}{3}\)
\(\Rightarrow\left(-3\right).\left(-3\right)=2.\left(x+7\right)\)
\(\Rightarrow9=2x+14\)
\(\Rightarrow2x=-5\)
\(\Rightarrow x=-\dfrac{5}{2}\)

a: ΔDEF đều
=>DE=DF=EF và \(\widehat{DEF}=\widehat{EDF}=\widehat{DFE}=60^0\)
EM là phân giác của góc DEF
=>\(\widehat{DEM}=\widehat{FEM}=\dfrac{\widehat{DEF}}{2}=30^0\)
Ta có: ΔDEP vuông tại D
=>\(\widehat{DEP}+\widehat{DPE}=90^0\)
=>\(\widehat{DPE}=90^0-60^0=30^0\)
Xét ΔNEP có \(\widehat{NEP}=\widehat{NPE}\left(=30^0\right)\)
nên ΔNEP cân tại N
b: Xét ΔDEN và ΔFEN có
DE=FE
\(\widehat{DEN}=\widehat{FEN}\)
EN chung
Do đó: ΔDEN=ΔFEN
=>\(\widehat{EDN}=\widehat{EFN}\)
=>\(\widehat{EFN}=90^0\)
=>NF\(\perp\)EP
c: ΔNEP cân tại N
mà NF là đường cao
nên F là trung điểm của EP

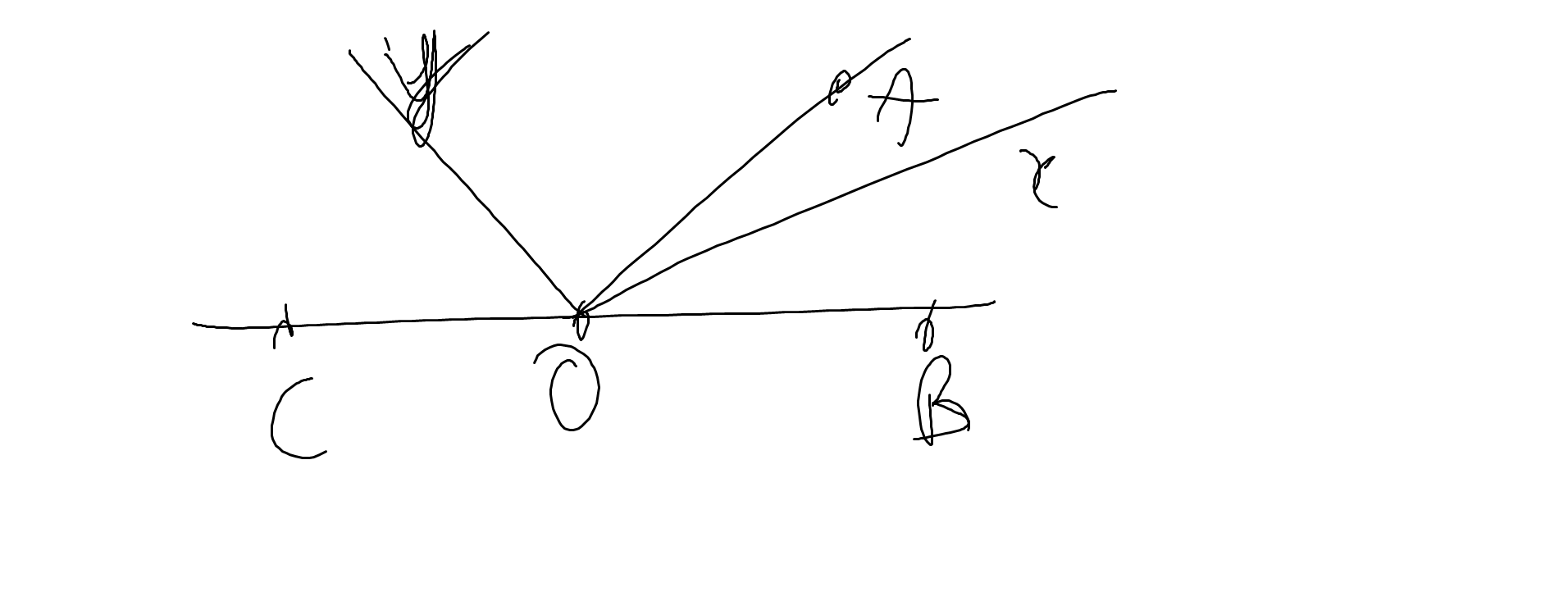
| GT | \(\widehat{AOB};\widehat{AOC}\) là hai góc kề bù Ox,Oy lần lượt là phân giác của góc AOB,góc AOC |
| KL | Ox\(\perp\)Oy |
Ox là phân giác của góc BOA
=>\(\widehat{xOA}=\dfrac{\widehat{BOA}}{2}\)
Oy là phân giác của góc COA
=>\(\widehat{yOA}=\dfrac{\widehat{COA}}{2}\)
\(\widehat{xOy}=\widehat{xOA}+\widehat{yOA}=\dfrac{1}{2}\left(\widehat{BOA}+\widehat{COA}\right)\)
\(=\dfrac{1}{2}\cdot180^0=90^0\)
=>Ox\(\perp\)Oy
cíu mình với