xác định hệ số a và b sao cho :x^3+ax+b chia hết cho x^2+4x+3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi cạnh của hình lập phương đó là `x (cm)`
Điều kiện: `x > 0`
Diện tích toán phần của hình lập phương là:
`x . x . 6 = 6x^2`
Thể tích hình lập phương là:
`x . x . x = x^3`
Mà diện tích toàn phần của hình lập phương bằng thể tích của nó
`=> x^3 = 6x^2`
`=> x^3 - 6x^2 = 0`
`=> x^2 (x - 6) = 0`
`=> x = 0` hoặc `x = 6`
Mà `x > 0` nên `x = 6`
Vậy cạnh của hình lập phương là `6cm`
Thể tích hình lập phương là:
`6^3 = 216 (cm^3)`
Vậy ....

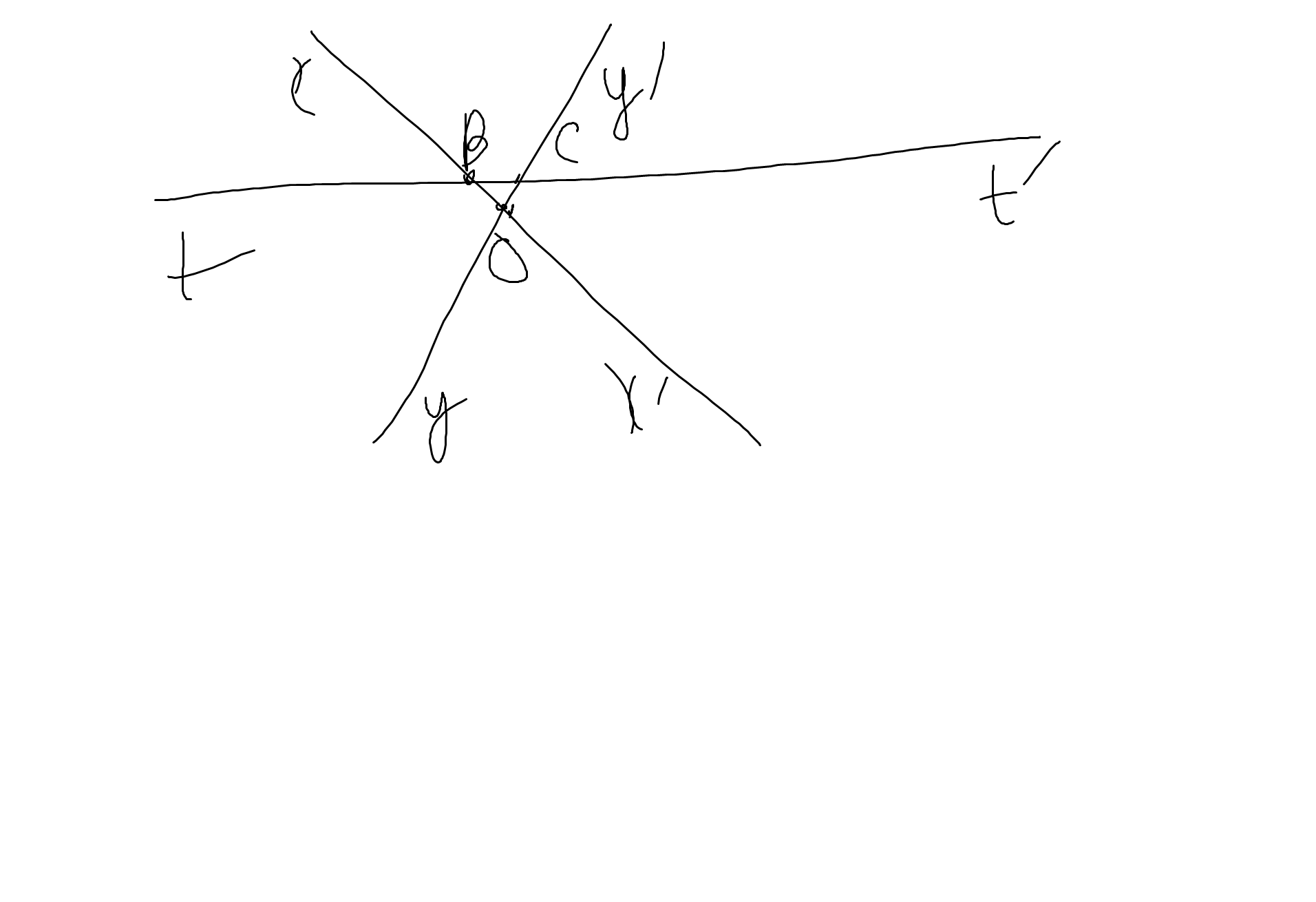
Bài 3: Các cặp góc so le trong là: \(\widehat{tBO};\widehat{BOC}\); \(\widehat{OBC};\widehat{yOB}\); \(\widehat{BCO};\widehat{x'OC}\); \(\widehat{t'CO};\widehat{BOC}\)
Các cặp góc đồng vị là:
\(\widehat{xBt};\widehat{xOy}\); \(\widehat{tBO};\widehat{x'Oy}\); \(\widehat{y'Ct'};\widehat{x'Oy'}\); \(\widehat{t'CO};\widehat{x'Oy}\)
Bài 2:
Các cặp góc so le trong là \(\widehat{FEC};\widehat{ACB}\)
Các cặp góc đồng vị là \(\widehat{ADE};\widehat{ABC}\); \(\widehat{AED};\widehat{ACB}\)
Các cặp góc trong cùng phía là: \(\widehat{BDE};\widehat{B}\); \(\widehat{DEC};\widehat{ECB}\)

Ta thấy
b - 1 < b < b + 1
=> b - 1; b; b + 1 là 3 số tự nhiên liên tiếp sắp xếp theo thứ tự tăng dần
m < m + 1 < m + 2
=> m; m + 1; m + 2 là 3 số tự nhiên liên tiếp sắp xếp theo thứ tự tăng dần
n + 1 < n + 2 < n + 3
=> n + 1; n + 2; n + 3 là 3 số tự nhiên liên tiếp sắp xếp theo thứ tự tăng dần
c + 1 > c > c - 1
=> c + 1; c; c - 1 là 3 số tự nhiên liên tiếp sắp xếp theo thứ tự giảm dần
Chọn phương án số 2

`-1/3<=x/3<=-1/6`
`=>-2/6<=2x/3<=-1/6`
`=>-2<=2x<=-1`
`=>-2/2<=x<=-1/2`
`=>-1<=x<=-1/2`
\(\dfrac{-1}{2}< \dfrac{x}{3}< \dfrac{-1}{6}\)
`=>` \(\dfrac{-3}{6}< \dfrac{2x}{6}< \dfrac{-1}{6}\)
`=> -3 < 2x < -1`
Mà `2x` là số nguyên
`=> 2x = -2`
`=> x = -1`
Vậy `x = -1`

`4^3<=2^x<=2^10`
`=>(2^2)^3<=2^x<=2^10`
`=>2^(2*3)<=2^x<=2^10`
`=>2^6<=2^x<=2^10`
`=>6<=x<=10`

a: Ta có: ΔABC vuông tại A
=>\(BC^2=AB^2+AC^2\)
=>\(BC=\sqrt{4^2+3^2}=5\left(cm\right)\)
Xét ΔABC vuông tại A có
\(sinB=\dfrac{AC}{BC}=\dfrac{3}{5};cosB=\dfrac{AB}{BC}=\dfrac{4}{5}\)
b: Xét ΔABC vuông tại A có AH là đường cao
nên \(\left\{{}\begin{matrix}AH\cdot BC=AB\cdot AC\\BH\cdot BC=BA^2\\CH\cdot CB=CA^2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}AH\cdot5=3\cdot4=12\\BH\cdot5=4^2=16\\CH\cdot5=3^2=9\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AH=2,4\left(cm\right)\\BH=3,2\left(cm\right)\\CH=1,8\left(cm\right)\end{matrix}\right.\)
Xét ΔAHB vuông tại H có HK là đường cao
nên \(AK\cdot AB=AH^2\)
=>\(AK\cdot4=2,4^2\)
=>\(AK=1,44\left(cm\right)\)
Xét ΔAHC vuông tại H có HI là đường cao
nên \(AI\cdot AC=AH^2\)
=>\(AI=\dfrac{2.4^2}{3}=1,92\left(cm\right)\)
c: xét tứ giác AIHK có \(\widehat{AIH}=\widehat{AKH}=\widehat{KAI}=90^0\)
=>AIHK là hình chữ nhật
=>\(S_{AIHK}=AI\cdot AK=1,92\cdot1,44=2,7648\left(cm^2\right)\)

Đề của bạn cho là phương trình, không phải đa thức. Bạn xem lại nhé.
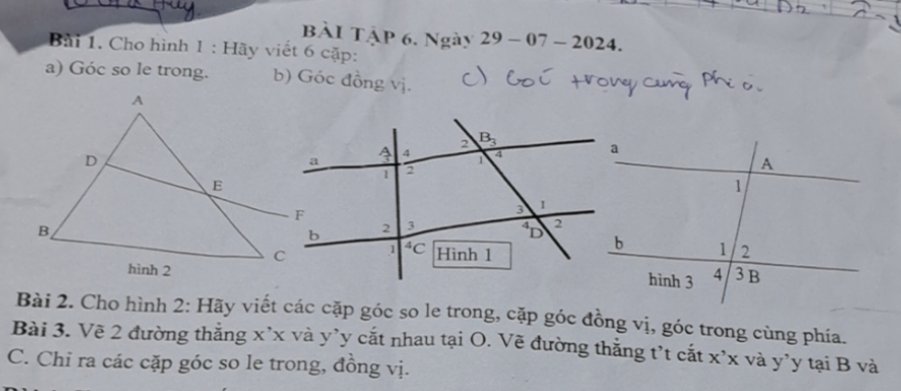

\(x^3+ax+b\\ =\left(x^3+4x^2+3x\right)+\left(-4x^2-16x-12\right)+\left(a+13\right)x+\left(b+12\right)\\ =x\left(x^2+4x+3\right)-4\left(x^2+4x+3\right)+\left(a+13\right)x+\left(b+12\right)\\ =\left(x-4\right)\left(x^2+4x+3\right)+\left(a+13\right)x+\left(b+12\right)\)
Để `x^3+ax+b` chia hết cho `x^2+4x+3` thì:
\(\left\{{}\begin{matrix}a+13=0\\b+12=0\end{matrix}\right.=>\left\{{}\begin{matrix}a=-13\\b=-12\end{matrix}\right.\)