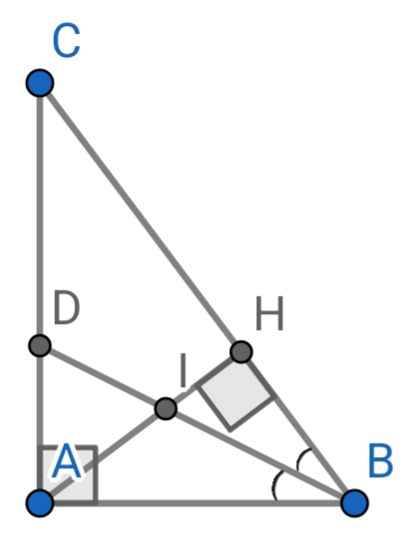
Cho tam giác nhọn ABC có 3 đường cao AD, BE, CF cắt nhau tại H.
a) Gọi G, I, K, P thứ tự là hình chiếu của D trên BA, BE, CF, CA. Chứng minh rằng 4 điểm G, I, K, P thẳng hàng.
b) Gọi O. M thứ tự là hình chiếu của E, F trên CF, BE. Chứng minh OM vuông góc với AD