tìm a để pt x^2+4x+4a-a^2=0 có hai nghiệm x1, x2 thỏa mãn x1^3-x2^3+2x1^2+8x1+31=0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi thời gian đi từ A đến B là x(giờ)
(ĐK: x>0)
Thời gian đi từ B đến C là x+0,5(giờ)
Độ dài quãng đường từ A đến B là 10x(km)
Độ dài quãng đường từ B đến C là 9(x+0,5)(km)
Độ dài AC là 33km nên ta có:
10x+9(x+0,5)=33
=>19x+4,5=33
=>19x=33-4,5=30-1,5=28,5
=>x=1,5(nhận)
vậy: Thời gian đi từ A đến B là 1,5 giờ
Thời gian đi từ B đến C là 1,5+0,5=2 giờ

a: Xét tứ giác ABOC có \(\widehat{OBA}+\widehat{OCA}=90^0+90^0=180^0\)
nên ABOC là tứ giác nội tiếp đường tròn đường kính OA
tâm là trung điểm của OA
b: Xét (O) có
\(\widehat{ABD}\) là góc tạo bởi tiếp tuyến BA và dây cung BD
\(\widehat{BED}\) là góc nội tiếp chắn cung BD
Do đó: \(\widehat{ABD}=\widehat{BED}\)
mà \(\widehat{BED}=\widehat{DAK}\)(hai góc so le trong, BE//AC)
nên \(\widehat{KAD}=\widehat{KBA}\)
Xét ΔKAD và ΔKBA có
\(\widehat{KAD}=\widehat{KBA}\)
\(\widehat{AKD}\) chung
Do đó: ΔKAD~ΔKBA
=>\(\dfrac{KA}{KB}=\dfrac{KD}{KA}\)
=>\(KA^2=KB\cdot KD\)
Xét (O) có
\(\widehat{KCD}\) là góc tạo bởi tiếp tuyến CK và dây cung CD
\(\widehat{CBD}\) là góc nội tiếp chắn cung CD
Do đó: \(\widehat{KCD}=\widehat{CBD}\)
Xét ΔKCD và ΔKBC có
\(\widehat{KCD}=\widehat{KBC}\)
\(\widehat{CKD}\) chung
Do đó: ΔKCD~ΔKBC
=>\(\dfrac{KC}{KB}=\dfrac{KD}{KC}\)
=>\(KC^2=KB\cdot KD\)
=>KC=KA
=>K là trung điểm của AC

a: Xét (O) có
\(\widehat{ACB}\) là góc nội tiếp chắn cung AB
Do đó: \(\widehat{ACB}=\dfrac{1}{2}\cdot sđ\stackrel\frown{AB}=45^0\)
Xét tứ giác ANMB có \(\widehat{ANB}=\widehat{AMB}=90^0\)
nên ANMB là tứ giác nội tiếp
b: Xét (O) có \(\widehat{BNA}\) là góc có đỉnh ở bên trong đường tròn chắn hai cung BA và CE
=>\(\widehat{BNA}=\dfrac{1}{2}\cdot\left(sđ\stackrel\frown{BA}+sđ\stackrel\frown{CE}\right)\)
=>\(sđ\stackrel\frown{BA}+sđ\stackrel\frown{CE}=90^0\cdot2=180^0\)
=>\(sđ\stackrel\frown{CE}=90^0\)
Xét (O) có \(\widehat{BMA}\) là góc có đỉnh ở bên trong đường tròn chắn hai cung BA và DC
=>\(\widehat{BMA}=\dfrac{1}{2}\left(sđ\stackrel\frown{BA}+sđ\stackrel\frown{CD}\right)\)
=>\(sđ\stackrel\frown{CD}+90^0=2\cdot\widehat{BMA}=180^0\)
=>\(sđ\stackrel\frown{CD}=90^0\)
\(sđ\stackrel\frown{ED}=sđ\stackrel\frown{CD}+sđ\stackrel\frown{DE}=90^0+90^0=180^0\)
=>E,O,D thẳng hàng
=>DE là đường kính của (O)
Xét (O) có
ΔDAE nội tiếp
DE là đường kính
Do đó; ΔDAE vuông tại A
=>DA\(\perp\)IE tại A
mà DA\(\perp\)BC
nên BC//IA
Xét (O) có
ΔDBE nội tiếp
DE là đường kính
Do đó: ΔDBE vuông tại C
=>DB\(\perp\)BE
mà BE\(\perp\)CA
nên DB//CA
Xét tứ giác ACBI có
AC//BI
AI//BC
Do đó: ACBI là hình bình hành

Gọi chiều dài của mảnh vườn là: \(x\left(m\right)\)
chiều rộng của mảnh vườn là: \(y\left(m\right)\)
ĐK: \(x,y>0\)
Chu vi của mảnh vườn là 130m ta có:
\(\left(x+y\right)\cdot2=130\Leftrightarrow x+y=\dfrac{130}{2}=65\left(1\right)\)
Hai lần chiều dài hơn ba lần chiều rộng 35m nên ta có:
\(2x-3y=35\left(2\right)\)
Từ (1) và (2) ta có hpt:
\(\left\{{}\begin{matrix}x+y=65\\2x-3y=35\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x+2y=130\\2x-3y=35\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}5y=95\\x+y=65\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=19\\x=65-19=46\end{matrix}\right.\left(tm\right)\)
Diện tích của mảnh vườn là: \(19\cdot46=874\left(m^2\right)\)

Chỗ kia phải là \(\dfrac{c^4}{b+a+4ba}\) chứ nhỉ? Nếu đúng đề thì bạn nói với mình để mình làm lại nhé. Giờ mình làm theo đề đối xứng trước nhé.
Ta có:
\(P=\dfrac{a^6}{a^2b+a^2c+4a^2bc}+\dfrac{b^6}{b^2a+b^2c+4b^2ca}+\dfrac{c^6}{c^2a+c^2b+4c^2ab}\)
\(\ge\dfrac{\left(a^3+b^3+c^3\right)^2}{a^2b+b^2c+c^2a+ab^2+bc^2+ca^2+4a^2bc+4b^2ca+4c^2ab}\)
\(=\dfrac{9}{\left(a+b+c\right)\left(ab+bc+ca\right)+abc\left(4\left(a+b+c\right)-3\right)}\)
Ta có \(ab+bc+ca\le\dfrac{\left(a+b+c\right)^2}{3}\)
và \(abc\le\dfrac{a^3+b^3+c^3}{3}=1\), đồng thời \(\left(a+b+c\right)^3=a^3+b^3+c^3+3\left(a+b\right)\left(b+c\right)\left(c+a\right)=3+3\left(a+b\right)\left(b+c\right)\left(c+a\right)>\dfrac{27}{64}\)
\(\Leftrightarrow a+b+c>\dfrac{3}{4}\) \(\Leftrightarrow4\left(a+b+c\right)-3>0\). Do đó \(abc\left(4\left(a+b+c\right)-3\right)\le4\left(a+b+c\right)-3\)
Vì vậy \(P\ge\dfrac{9}{\dfrac{\left(a+b+c\right)^3}{3}+4\left(a+b+c\right)-3}\)
Đặt \(a+b+c=t\).
Ta có \(a^3+b^3\ge ab\left(a+b\right)=a^2b+b^2a\). Lập 2 BĐT tương tự rồi cộng theo vế, ta có:
\(2\left(a^3+b^3+c^3\right)\ge a^2b+b^2c+c^2a+ab^2+bc^2+ca^2\)
\(\Leftrightarrow\left(a+b\right)\left(b+c\right)\left(c+a\right)\le6+2abc\le8\) (vì \(abc\le1\))
Do đó \(t^3=3+3\left(a+b\right)\left(b+c\right)\left(c+a\right)\le3+3.8=27\) \(\Leftrightarrow t\le3\)
Vậy \(0< t\le3\)
Ta có \(P\ge\dfrac{9}{\dfrac{t^3}{3}+4t-3}\) \(\ge\dfrac{9}{\dfrac{3^3}{3}+4.3-3}=\dfrac{1}{2}\)
Dấu "=" xảy ra khi \(a=b=c=1\)
Vậy GTNN của P là \(\dfrac{1}{2}\) khi \(a=b=c=1\)

\(\text{Δ}=\left[-2\left(m-1\right)\right]^2-4\cdot1\cdot\left(-4m\right)\)
\(=4\left(m^2-2m+1\right)+16m\)
\(=4m^2+8m+4=\left(2m+2\right)^2>=0\forall m\)
Để phương trình có hai nghiệm phân biệt thì Δ>0
=>(2m+2)^2>0
=>\(2m+2\ne0\)
=>\(2m\ne-2\)
=>\(m\ne-1\)
Theo vi-et, ta có:
\(x_1+x_2=-\dfrac{b}{a}=2\left(m-1\right);x_2x_1=-4m\)
\(\left|x_1-x_2\right|=2022\)
=>\(\sqrt{\left(x_1-x_2\right)^2}=2022\)
=>\(\sqrt{\left(x_1+x_2\right)^2-4x_1x_2}=2022\)
=>\(\sqrt{\left(2m-2\right)^2-4\cdot\left(-4m\right)}=2022\)
=>\(\sqrt{\left(2m+2\right)^2}=2022\)
=>\(\left|2m+2\right|=2022\)
=>|m+1|=1011
=>\(\left[{}\begin{matrix}m+1=1011\\m+1=-1011\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=1010\left(nhận\right)\\m=-1012\left(nhận\right)\end{matrix}\right.\)

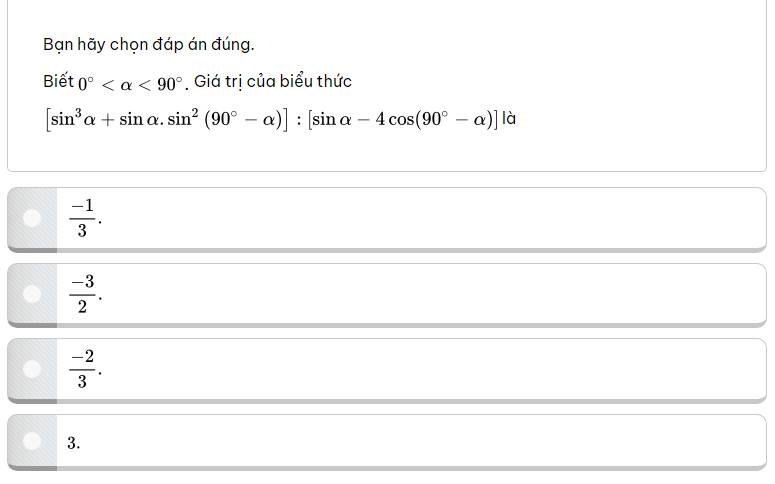
\(\left[sin^3a+sina\cdot sin^2\left(90-a\right)\right]:\left[sina-4\cdot cos\left(90-a\right)\right]\)
\(=\left[sin^3a+sina\cdot cos^2a\right]:\left[sina-4\cdot sina\right]\)
\(=\dfrac{sina\left(sin^2a+cos^2a\right)}{-3\cdot sina}=\dfrac{1}{-3}=-\dfrac{1}{3}\)