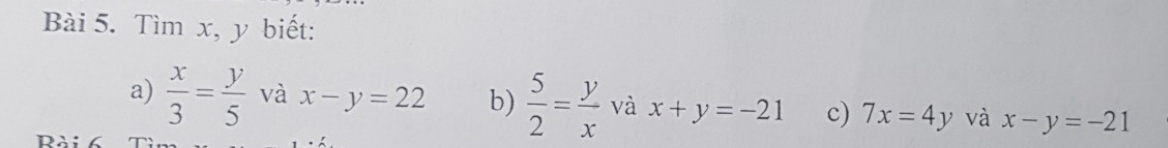 giúp e ạ
giúp e ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 11: \(\dfrac{2a+13b}{3a-7b}=\dfrac{2c+13d}{3c-7d}\)
=>\(\left(2a+13b\right)\left(3c-7d\right)=\left(3a-7b\right)\left(2c+13d\right)\)
=>\(6ac-14ad+39bc-91bd=6ac+39ad-14bc-91bd\)
=>-14ad-39ad=-14bc-39bc
=>ad=bc
=>\(\dfrac{a}{b}=\dfrac{c}{d}\)
Bài 12:
\(\dfrac{a+2019}{a-2019}=\dfrac{b+2020}{b-2020}\)
=>\(\left(a+2019\right)\left(b-2020\right)=\left(a-2019\right)\left(b+2020\right)\)
=>\(ab-2020a+2019b-2019\cdot2020=ab+2020a-2019b-2019\cdot2020\)
=>-2020a-2020a=-2019b-2019b
=>2020a=2019b
=>\(\dfrac{a}{2019}=\dfrac{b}{2020}\)

\(\left(x-4\right)^2\left(x+4\right)-\left(x-4\right)\left(x+4\right)^2+3\left(x^2-16\right)\)
\(=\left(x^2-16\right)\left(x-4\right)-\left(x^2-16\right)\left(x+4\right)+3\left(x^2-16\right)\)
\(=\left(x^2-16\right)\left(x-4-x-4+3\right)\)
\(=-5\left(x^2-16\right)=-5x^2+80\)

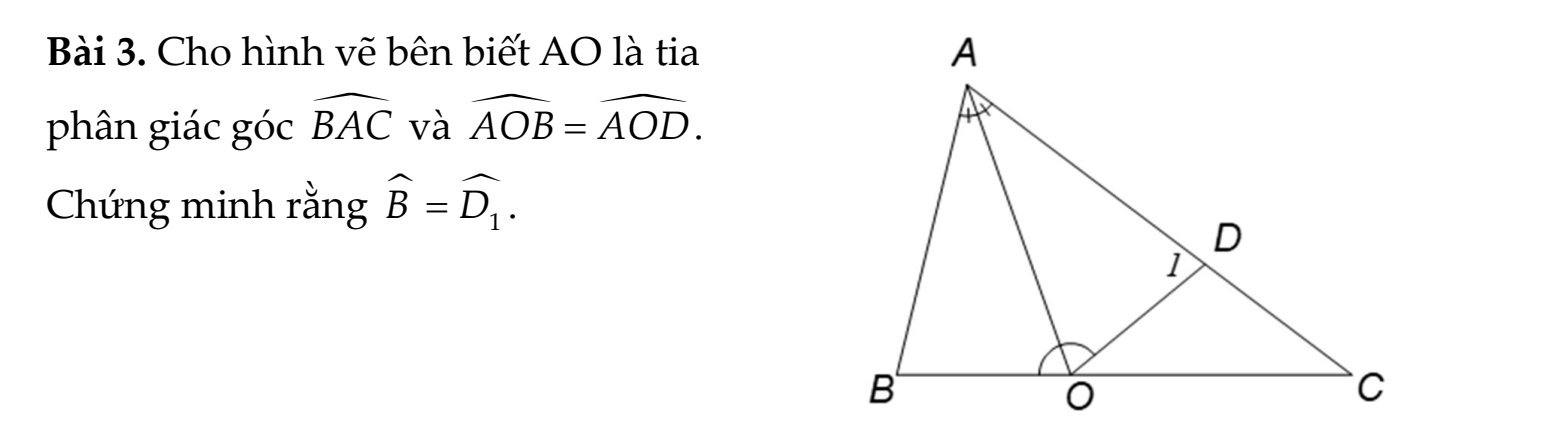
Xét 2 ΔABO và ΔADO ta có:
\(\widehat{BAO}=\widehat{DAO}\) (AD là phân giác của góc BAC)
\(OA\) chung
\(\widehat{AOB}=\widehat{AOD}\left(gt\right)\)
\(=>\Delta ABO=\Delta ADO\left(g.c.g\right)\)
\(=>\widehat{B}=\widehat{D_1}\) (hai góc tương ứng)

ΔABC cân tại A
=>\(\widehat{BAC}=180^0-2\cdot\widehat{ABC}=100^0\)
AD là phân giác góc ngoài tại đỉnh A
=>\(\widehat{CAD}=\dfrac{180^0-\widehat{BAC}}{2}=40^0\)
=>\(\widehat{CAD}=\widehat{ACB}\left(=40^0\right)\)
mà hai góc này là hai góc ở vị trí so le trong
nên AD//BC

Xét ΔABC vuông tại A có \(\widehat{ABC}+\widehat{ACB}=90^0\)
=>\(2\cdot\left(\widehat{OBC}+\widehat{OCB}\right)=90^0\)
=>\(\widehat{OBC}+\widehat{OCB}=45^0\)
Xét ΔOBC có \(\widehat{BOC}+\widehat{OBC}+\widehat{OCB}=180^0\)
=>\(\widehat{BOC}+45^0=180^0\)
=>\(\widehat{BOC}=135^0\)

\(\widehat{A}=180^o-\widehat{B}-\widehat{C}=180^o-40^o-40^o=100^o\)
=> \(\widehat{A_{ngoai}}=180^o-100^o=80^o\)
=> \(\widehat{DAB}=\dfrac{1}{2}\widehat{A_{ngoai}}=\dfrac{1}{2}\cdot80^o=40^o\)
Ta có: \(\widehat{DAB}=\widehat{ABC}\left(=40^o\right)\)
Mà 2 góc này ở vị trí so le trong
=> AD//BC

\(\left(2,5x-\dfrac{4}{7}\right):\dfrac{8}{21}=-1,5\)
=>\(\left(\dfrac{5}{2}x-\dfrac{4}{7}\right):\dfrac{8}{21}=-\dfrac{3}{2}\)
=>\(\dfrac{5}{2}x-\dfrac{4}{7}=\dfrac{-3}{2}\cdot\dfrac{8}{21}=\dfrac{-24}{42}=\dfrac{-4}{7}\)
=>\(\dfrac{5}{2}x=-\dfrac{4}{7}+\dfrac{4}{7}=0\)
=>x=0

\(2^2+3^2+...+2021^2\)
\(=\left(1^2+2^2+...+2021^2\right)-1\)
\(=\dfrac{2021\cdot\left(2021+1\right)\left(2\cdot2021+1\right)}{6}=1\)
\(=2753594310\)

1: \(5^{x+4}-3\cdot5^{x+3}=2\cdot5^{11}\)
=>\(5^{x+3}\cdot5-3\cdot5^{x+3}=2\cdot5^{11}\)
=>\(2\cdot5^{x+3}=2\cdot5^{11}\)
=>x+3=11
=>x=8
2: \(\dfrac{1}{2}\cdot2^x+4\cdot2^x=9\cdot2^5\)
=>\(2^x\cdot\left(\dfrac{1}{2}+4\right)=9\cdot2^5\)
=>\(2^x\cdot\dfrac{9}{2}=9\cdot2^5\)
=>\(2^x=2^6\)
=>x=6
3: \(9^{2x+1}=27^3\)
=>\(3^{4x+2}=3^9\)
=>4x+2=9
=>4x=7
=>\(x=\dfrac{7}{4}\)
4: \(2^{-1}\cdot2^x+4\cdot2^x=9\cdot2^5\)
=>\(2^x\left(4+\dfrac{1}{2}\right)=9\cdot2^5\)
=>\(2^x\cdot\dfrac{9}{2}=9\cdot2^5\)
=>\(2^x=9\cdot2^5:\dfrac{9}{2}=2^6\)
=>x=6
5: \(\left(2x-1\right)^3=\dfrac{8}{27}\)
=>\(\left(2x-1\right)^3=\left(\dfrac{2}{3}\right)^3\)
=>\(2x-1=\dfrac{2}{3}\)
=>\(2x=\dfrac{2}{3}+1=\dfrac{5}{3}\)
=>\(x=\dfrac{5}{3}:2=\dfrac{5}{6}\)
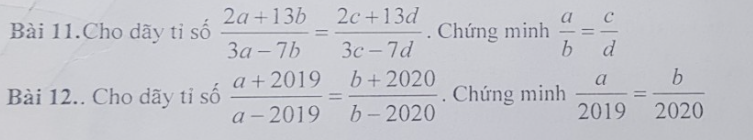



a, Theo tc dãy tỉ số bằng nhau
\(\dfrac{x}{3}=\dfrac{y}{5}=\dfrac{x-y}{3-5}=\dfrac{22}{-2}=-11\Rightarrow x=-33;y=-55\)
b, \(\dfrac{5}{2}=\dfrac{y}{x}\Rightarrow\dfrac{x}{2}=\dfrac{y}{5}\)Theo tc dãy tỉ số bằng nhau
\(\dfrac{x}{2}=\dfrac{y}{5}=\dfrac{x+y}{2+5}=-\dfrac{21}{7}=-3\Rightarrow x=-6;y=-15\)
c, \(7x=4y\Rightarrow\dfrac{x}{4}=\dfrac{y}{7}\)Theo tc dãy tỉ số bằng nhau
\(\dfrac{x}{4}=\dfrac{y}{7}=\dfrac{x-y}{3-7}=-\dfrac{21}{-4}=7\Rightarrow x=28;y=49\)