Ta có : \(P=\sqrt{2x^2+xy+2y^2}+\sqrt{2y^2+yz+2z^2}+\sqrt{2z^2+xz+2x^2}\)

Xét : \(\sqrt{2x^2+xy+2y^2}=\sqrt{\dfrac{3}{4}.\left(x-y\right)^2+\dfrac{5}{4}.\left(x+y\right)^2}\)

\(\ge\sqrt{\dfrac{5}{4}.\left(x+y\right)^2}=\dfrac{\sqrt{5}}{2}.\left(x+y\right)\)

\(CMTT:\sqrt{2y^2+yz+2z^2}\ge\dfrac{\sqrt{5}}{2}.\left(y+z\right)\)

                \(\sqrt{2z^2+xz+2x^2}\ge\dfrac{\sqrt{5}}{2}.\left(x+z\right)\)

Do đó : \(P\ge\dfrac{\sqrt{5}}{2}.\left(x+y+y+z+z+x\right)=\dfrac{2\sqrt{5}.\left(x+y+z\right)}{2}\)

\(\Rightarrow P\ge\sqrt{5}.\left(x+y+z\right)\)

Ta có : BĐT : \(\left(a+b+c\right)^2\ge3\left(ab+bc+ca\right)\)

\(\Rightarrow\left(x+y+z\right)^2\ge3\left(xy+yz+zx\right)\)

Mà : \(xy+yz+zx=3\)

\(\Rightarrow\left(x+y+z\right)^2\ge9\)

\(\Leftrightarrow x+y+z\ge3\)

\(\Rightarrow P_{min}=3\sqrt{5}\)

Dấu bằng xảy ra : \(\Leftrightarrow x=y=z=1\)

\(\sqrt{x-2}+\sqrt{6-x}\text{=}\sqrt{x^2-8x+24}\)

\(ĐKXĐ:2\le x\le6\)

Xét VP của pt ta thấy : \(\sqrt{x^2-8x+24}\text{=}\sqrt{x^2-8x+16+8}\)

\(\text{=}\sqrt{\left(x-4\right)^2+8}\)

\(\Rightarrow VP\ge\sqrt{8}\)

Xét VT của pt ta có :

\(VT^2\text{=}x-2+6-x+2\sqrt{\left(x-2\right)\left(6-x\right)}\)

\(VT^2\text{=}4+2\sqrt{\left(x-2\right)\left(6-x\right)}\)

Áp dụng BĐT cô si cho 2 số không âm ta có :

\(2\sqrt{\left(x-2\right)\left(6-x\right)}\le\left(\sqrt{x-2}\right)^2+\left(\sqrt{6-x}\right)^2\)

\(\text{=}x-2+6-x\text{=}4\)

\(\Rightarrow VT^2\le8\)

\(\Rightarrow VT\le\sqrt{8}\)

Để \(VT\text{=}VP\) \(\Leftrightarrow\left\{{}\begin{matrix}x-4\text{=}0\\\sqrt{x-2}\text{=}\sqrt{6-x}\end{matrix}\right.\)

\(\Leftrightarrow x=4\left(TM\right)\)

Vậy...........

Bạn có thể giảm số phương trình hoá học đi được không ạ.

mình xin lỗi nhưng cô mình bảo vậy

ai làm được thì giúp mình

d3//d1 => a=2 (b khác 1)

d3 cắt d2 tại điểm có tung độ bằng 2 Thay y=2 vào d2

=> 2=-x+4=> x=2 Thay y=2; x=2; a=2 vào d3

=> 2+2.2+b=> b=-6

CaO mang tính chất oxit base (tác dụng oxit axit, tác dụng dung dịch axit, tác dụng với nước tạo dung dịch base)

Còn SO₂ mang tính chất oxit axit (tác dụng oxit base, tác dụng với dung dịch base, tác dụng với nước tạo dung dịch axit kém bền)

a

lêu

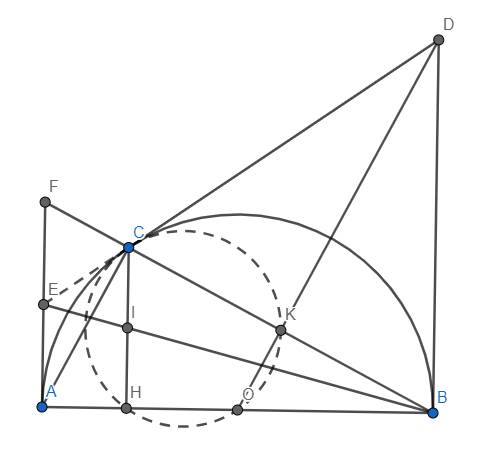
a) Ta thấy OK là đường trung bình của tam giác ABC \(\Rightarrow\) OK//AC.

Mà \(AC\perp CB\) tại C nên \(OK\perp BC\) tại K hay \(DK\perp BC\) tại K

 Tam giác BCD có DK vừa là đường cao, vừa là trung tuyến nên tam giác BCD cân tại D, suy ra \(DB=DC\) (đpcm)

 Dễ dàng chứng minh \(\Delta OBD=\Delta OCD\left(c.c.c\right)\) \(\Rightarrow\widehat{OCD}=\widehat{OBD}=90^o\), suy ra DC tiếp xúc với (O) tại C. (đpcm)

 b) Tứ giác OHCK có \(\widehat{CHO}+\widehat{CKO}=90^o+90^o=180^o\) nên OHCK nội tiếp, điều này có nghĩa là \(C\in\left(OHK\right)\) (đpcm)

 c) Gọi F là giao điểm của BC và AE. Do CH//AF nên theo bổ đề hình thang, E là trung điểm của AF.

 Tam giác CAF vuông tại C có trung tuyến CE nên \(CE=\dfrac{1}{2}AF=EA\), suy ra tam giác ACE cân tại E 

 \(\Rightarrow\widehat{ECA}=\widehat{EAC}\)

Mặt khác, EA tiếp xúc với (O) tại A nên \(\widehat{EAC}=\dfrac{1}{2}sđ\stackrel\frown{AC}\)

Từ đó suy ra \(\widehat{EAC}=\dfrac{1}{2}sđ\stackrel\frown{AC}\) \(\Rightarrow\) EC tiếp xúc với (O) tại C.

Mà DC cũng tiếp xúc với (O) tại C nên D, E, C thẳng hàng (đpcm)

Bài 4:

Ta có \(\dfrac{1}{a^2\left(b+c\right)}=\dfrac{abc}{a^2\left(b+c\right)}=\dfrac{bc}{ab+ca}\)

Tương tự: \(\dfrac{1}{b^2\left(c+a\right)}=\dfrac{ca}{bc+ab}\) và \(\dfrac{1}{c^2\left(a+b\right)}=\dfrac{ab}{bc+ca}\)

Đặt \(\left\{{}\begin{matrix}bc=x\\ca=y\\ab=z\end{matrix}\right.\) với \(x,y,z>0;xyz=1\)

Khi đó BĐT cần chứng minh trở thành:

 \(\dfrac{x}{y+z}+\dfrac{y}{z+x}+\dfrac{z}{x+y}\ge\dfrac{3}{2}\) 

Thật vậy, đặt \(P=\dfrac{x}{y+z}+\dfrac{y}{z+x}+\dfrac{z}{x+y}\)

\(P=\dfrac{x^2}{xy+zx}+\dfrac{y^2}{yz+xy}+\dfrac{z^2}{zx+yz}\)

\(P\ge\dfrac{\left(x+y+z\right)^2}{2\left(xy+yz+zx\right)}\) (BĐT B.C.S)

Mà lại có \(xy+yz+zx\le\dfrac{\left(x+y+z\right)^2}{3}\) nên ta có:

\(P\ge\dfrac{\left(x+y+z\right)^2}{2.\dfrac{\left(x+y+z\right)^2}{3}}=\dfrac{3}{2}\) Vậy ta có đpcm. 

Dấu "=" xảy ra \(\Leftrightarrow x=y=z=1\) \(\Leftrightarrow a=b=c=1\)

P1: AA  x AA => F1(P1): 100% AA (Mắt đen 100%)

P2: AA x Aa => F1(P2): 1AA: 1Aa (Mắt đen 100%)

P3: AA x aa => F1(P3): 100% Aa (Mắt đen 100%)

P4: Aa x Aa => F1(P4): 1AA:2Aa:1aa (3 Mắt đen: 1 mắt nâu)

P5: AA x aa : Như P3

P6: aa x aa => F1(P6): 100% aa (Mắt nâu 100%)

Để hát quốc ca đúng như quy định, học sinh phải thực hiện các yêu cầu sau: Tư thế khi hát quốc ca phải nghiêm trang, đứng thẳng, mắt nhìn thẳng vào hướng lá cờ tổ quốc. Phải giữ trật tự trước và sau khi hát quốc ca. Khi hát phải theo hiệu lệnh để việc đồng ca diễn ra đồng đều.

cụ nhất kokushibo cop mạng