Chứng minh rằng với a+b>c và |a-b|<c với a,b,c >0 thì phương trình bậc hai a^2x^2 +(a^2+b^2-c^2)x +b^2=0 vô nghiệm
ĐOẠN MK BÔI ĐỎ GIẢI THÍCH HỘ
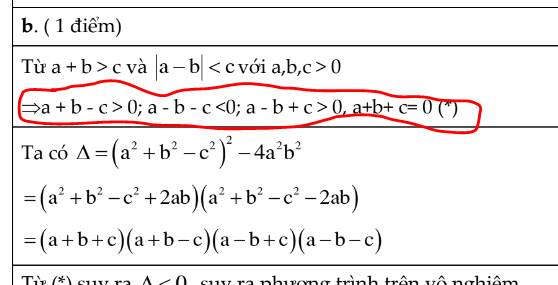
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1:
$\sqrt{x-4}-2$
ĐKXĐ: $x\geq 4$
Ta thấy $\sqrt{x-4}\geq 0$ với mọi $x\geq 4$
$\Rightarrow \sqrt{x-4}-2\geq 0-2=-2$
Vậy gtnn của biểu thức là $-2$. Giá trị này đạt được tại $x-4=0$
$\Leftrightarrow x=4$
Bài 2: $x-\sqrt{x}$
ĐKXĐ: $x\geq 0$
$x-\sqrt{x}=(x-\sqrt{x}+\frac{1}{4})-\frac{1}{4}=(\sqrt{x}-\frac{1}{2})^2-\frac{1}{4}$
$\geq 0-\frac{1}{4}=\frac{-1}{4}$
Vậy gtnn của biểu thức là $\frac{-1}{4}$. Giá trị này đạt được khi $\sqrt{x}-\frac{1}{2}=0$
$\Leftrightarrow x=\frac{1}{4}$

Quy ước : A: hoa đỏ
a : hoa trắng
TH1
P:hoa đỏ(AA) x hoa trắng(aa)
G: A a
F1; KG: Aa
KH: 100% đỏ
Th2 :
P: hoa đỏ( Aa) x hoa trắng( aa)
G: A,a a
F1: KG: 1Aax1aa
KH : 1 đỏ : 1 trắng
TH1:
F1: Aa(100%)__Hoa đỏ(100%)
TH2:
F1: 1Aa:1aa__50% hoa đỏ: 50% hoa trắng

Lời giải:
CM $\sqrt{a}+\sqrt{b}> \sqrt{a+b}$
BĐT cần chứng minh tương đương với:
$(\sqrt{a}+\sqrt{b})^2> a+b$
$\Leftrightarrow a+b+2\sqrt{ab}> a+b$
$\Leftrightarrow \sqrt{ab}>0$ (luôn đúng với mọi $a>0, b>0$)
Ta có đpcm
--------------------
CM $|a|+|b|> |a+b|$. Cái này là = rồi chứ không phải > bạn nhé.
Khi $a>0; b>0$ thì $|a|=a; |b|=b\Rightarrow |a|+|b|=a+b$
$|a+b|=a+b$
$\Rightarrow |a|+|b|=|a+b|$

Em học được từ Bác:
- Phong cách tư duy Hồ Chí Minh là độc lập, tự chủ, sáng tạo.
- Phong cách lãnh đạo của Hồ Chí Minh là tôn trọng nguyên tắc tập trung dân chủ, là thận trọng, chu đáo, sâu sát, tỉ mỉ, là lời nói phải đi đôi với việc làm...
- Hồ Chí Minh có sự giản dị, tiết kiệm và sự gần gũi, chan hoà với mọi người tạo nên phong cách giao tiếp riêng, rất lịch sự nhưng chân thành và ấm áp, bên cạnh phong cách đó là tình yêu thiên nhiên, tinh thần lạc quan của một người luôn biết làm chủ. Tình cảm đó chính là nguồn cảm xúc dồi dào để Người sáng tác những bài thơ nói về thiên nhiên, đất nước, con người. Với Hồ Chí Minh, khi hoạt động bí mật trong rừng sâu hay khi hoà bình về thành phố, thiên nhiên, với những “ mây, gió, trăng, hoa, tuyết, núi, sông” luôn gần gũi, gắn bó với cuộc sống của Người ...

Lời giải:
ĐKXĐ: $x\geq 0$
$-\sqrt{x}(\sqrt{x}-1)>0$
$\Leftrightarrow \sqrt{x}(\sqrt{x}-1)<0$
\(\Leftrightarrow \left[\begin{matrix} \left\{\begin{matrix} \sqrt{x}>0\\ \sqrt{x}-1<0\end{matrix}\right.\\ \left\{\begin{matrix} \sqrt{x}<0\\ \sqrt{x}-1>0\end{matrix}\right. (\text{TH này hiển nhiên vô lý})\end{matrix}\right. \)
\(\Leftrightarrow \left\{\begin{matrix} x>0\\ 0\leq x< 1\end{matrix}\right.\Leftrightarrow 0< x< 1\)
Lời giải:
Từ $a+b> c\Rightarrow a+b-c>0$ (cái này hiển nhiên)
Từ $|a-b|< c\Leftrightarrow |a-b|^2< c^2$
$\Leftrightarrow (a-b)^2< c^2$
$\Leftrightarrow (a-b-c)(a-b+c)<0$
Với $c>0$ thì $a-b-c< a-b+c$ nên để tích âm thì $a-b-c<0< a-b+c$
Hay $a-b-c<0$ và $a-b+c>0$