Tìm các số a, b thỏa mãn điều kiện: 11/17 < a/b < 23/29 và 8b - 9a = 31
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Số nguyên tố lẻ nhỏ nhất là số 3
=>a=3
Số chục là số nguyên tố chẵn
=>b=2
Số đơn vị là số nguyên tố duy nhất có tận cùng bằng 5
=>Hàng đơn vị là c=5
vậy: Số cần tìm là 325

Trên tia đối của tia NB, lấy E sao cho NB=NE
Xét ΔNBC và ΔNEA có
NB=NE
\(\widehat{BNC}=\widehat{ENA}\)(hai góc đối đỉnh)
NC=NA
Do đó: ΔNBC=ΔNEA
=>EC=EA
Xét ΔCBE có CB+CE>EB
mà CE=BA và EB=2BN
nên CB+BA>2BN


\(\dfrac{13}{8}-\dfrac{2}{9}+\dfrac{1}{2}=\dfrac{101}{72}+\dfrac{1}{2}=\dfrac{137}{12}\)

a: Để (d) có hệ số góc bằng -2 thì m-1=-2
=>m=-1
b: Thay x=-3 và y=0 vào (d), ta được:
\(-3\left(m-1\right)+2m=0\)
=>-3m+3+2m=0
=>3-m=0
=>m=3
c: Thay x=0 và y=2 vào (d), ta được:
0(m-1)+2m=2
=>2m=2
=>m=1
d: Để (d)//(d1) thì \(\left\{{}\begin{matrix}m-1=-3\\2m\ne4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m=-2\\m\ne2\end{matrix}\right.\)
=>m=-2
a) Tìm 𝑚m để 𝑑d có hệ số góc bằng -2.
Hệ số góc của đường thẳng 𝑑d là 𝑚−1m−1. Để 𝑑d có hệ số góc bằng -2, ta giải phương trình: 𝑚−1=−2
m−1=−2 𝑚=−2+1
\(\Rightarrow\)m=−2+1 𝑚=−1
\(\Rightarrow\)m=−1
b) Tìm 𝑚m để 𝑑d cắt trục hoành tại điểm có hoành độ bằng -3.
Khi 𝑑d cắt trục hoành, 𝑦=0y=0, từ đó: (𝑚−1)𝑥+2𝑚=0
(m−1)x+2m=0 (𝑚−1)(−3)+2𝑚=0
\(\Rightarrow\)(m−1)(−3)+2m=0 3(𝑚−1)+2𝑚=0
\(\Rightarrow\)3(m−1)+2m=0 3𝑚−3+2𝑚=0
\(\Rightarrow\)3m−3+2m=0 5𝑚−3=0
\(\Rightarrow\)5m−3=0 5𝑚=3
\(\Rightarrow\)5m=3 𝑚=35
\(\Rightarrow\)m= 3/5
c) Tìm 𝑚m để 𝑑d cắt trục tung tại điểm có tung độ bằng 2.
Khi 𝑑d cắt trục tung, 𝑥=0x=0, khi đó: (𝑚−1)⋅0+2𝑚=2
(m−1)⋅0+2m=2
\(\Rightarrow\)2𝑚=2\(\Rightarrow\)2m=2 𝑚=1
\(\Rightarrow\)m=1
d) Tìm 𝑚m để 𝑑d song song với đường thẳng 𝑑1d
: 𝑦=−3𝑥+4y=−3x+4.
Đường thẳng 𝑑d sẽ song song với 𝑑1d nếu hệ số góc của 𝑑d bằng hệ số góc của 𝑑1d: dđ𝑚−1=−3
\(\Rightarrow\) m−1=−3 𝑚=−3+1
\(\Rightarrow\)m=−3+1 𝑚=−2
\(\Rightarrow\)m=−2
Kết luận:a) 𝑚=−1m = -1
b) 𝑚=35m = 3/5
c) 𝑚=1m = 1
d) 𝑚=−2m = −2


Câu 3:
Ta thấy $\Delta'=(m^2+2)^2+2m^2+5>0$ với mọi $m\in\mathbb{R}$ nên PT luôn có 2 nghiệm pb với mọi $m$
Áp dụng định lý Viet:
$x_1+x_2=-2(m^2+2)$
$x_1x_2=-2m^2-5$
$\Rightarrow x_1x_2+1=x_1+x_2$
$\Leftrightarrow (x_1-1)(x_2-1)=0$
$\Leftrightarrow x_1=1$ hoặc $x_2=1$
Nếu $x_2=1$ thì $x_1=(-2m^2-5):x_2=-2m^2-5$
Mà $x_1>x_2$ nên $-2m^2-5>1$ (vô lý)
Do đó $x_1=1$. Khi đó $x_2=-2m^2-5$
Ta có:
$x_1x_2+8x_1^3+5=0$
$\Leftrightarrow -2m^2-5+8+5=0$
$\Leftrightarrow 8=2m^2$
$\Leftrightarrow m^2=4\Leftrightarrow m=\pm 2$

Chiến thắng Phát xít, hay còn gọi là Chiến thắng Đồng minh trong Chiến tranh Thế giới thứ hai, mang nhiều ý nghĩa to lớn đối với nhân loại, bao gồm:
1. Giữ gìn hòa bình và an ninh thế giới:
- Chiến thắng đã chấm dứt Chiến tranh Thế giới thứ hai, cuộc chiến tranh tàn khốc nhất trong lịch sử nhân loại, gây ra hơn 60 triệu người thiệt mạng và vô số tổn thất về vật chất.
- Chiến thắng góp phần ngăn chặn sự bành trướng của chủ nghĩa phát xít, chủ nghĩa quân phiệt, bảo vệ hòa bình và an ninh thế giới.
2. Thúc đẩy tự do và dân chủ:
- Chiến thắng đã giải phóng các dân tộc khỏi ách thống trị tàn bạo của chủ nghĩa phát xít, mở đường cho sự phát triển của tự do và dân chủ trên toàn thế giới.
- Chiến thắng góp phần thúc đẩy nhân quyền và các giá trị văn minh nhân loại.
3. Tạo điều kiện cho sự phát triển kinh tế - xã hội:
- Chiến thắng đã chấm dứt chiến tranh, tạo điều kiện cho các nước trên thế giới tập trung vào việc khôi phục và phát triển kinh tế - xã hội.
- Chiến thắng thúc đẩy hợp tác quốc tế và tạo ra môi trường thuận lợi cho giao thương, đầu tư.
4. Bài học lịch sử quý giá:
- Chiến thắng Phát xít là bài học lịch sử quý giá cho nhân loại về hậu quả thảm khốc của chiến tranh và tầm quan trọng của hòa bình.
- Chiến thắng nhắc nhở chúng ta về trách nhiệm chung trong việc bảo vệ hòa bình, an ninh thế giới và xây dựng một thế giới tốt đẹp hơn.
Đối với Việt Nam:
- Chiến thắng Phát xít góp phần quan trọng vào sự nghiệp giải phóng dân tộc của Việt Nam.
- Chiến thắng tạo điều kiện thuận lợi cho Cách mạng tháng Tám thành công, mở ra kỷ nguyên mới cho đất nước Việt Nam.
Nhìn chung, Chiến thắng Phát xít là một sự kiện lịch sử trọng đại có ý nghĩa to lớn đối với toàn nhân loại. Chiến thắng đã mang lại hòa bình, tự do, dân chủ và thúc đẩy sự phát triển kinh tế - xã hội trên toàn thế giới.
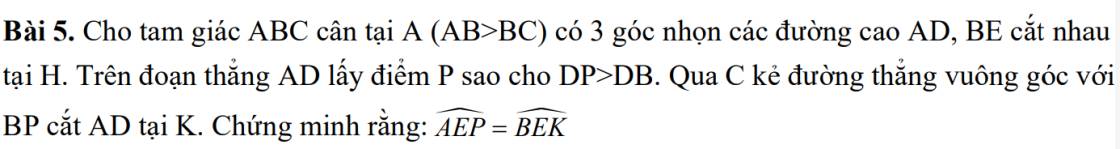


Ta biết:\(\dfrac{11}{17}\)<\(\dfrac{a}{b}< \dfrac{23}{29}\) và \(8b-9a=31\)(\(a,b\in N\))
\(\Rightarrow b=\dfrac{31+9a}{8}=\dfrac{32-1+8a+a}{8}=\left[\left(4+a\right)+\dfrac{a-1}{8}\right]\in N\)
⇒\(\dfrac{a-1}{8}\in N\)
\(\Leftrightarrow\left(a-1\right)⋮8\Rightarrow a=8k++1\)
khi đó\(b=\dfrac{31+9.\left(8k+1\right)}{8}=9k+5\)⇒\(\dfrac{11}{17}< \dfrac{8k+1}{9k+5}< \dfrac{23}{29}\)
11.(9k+5)<17.(8k+1)⇔k>129.(8k+1)<23.(9k+5)⇔k<4⇒1<k<4
⇒kϵ{2;3}
k=2=>a=17
b=23
k=3=>a=25
b=32
kết luận:(a,b) là:(17,23);(25,32)