a:

ĐKXĐ: \(x\ne0;y\ne0\)

 \(\dfrac{\dfrac{1}{x}+\dfrac{1}{y}}{\dfrac{1}{x}-\dfrac{1}{y}}=\dfrac{x+y}{xy}:\dfrac{x-y}{xy}=\dfrac{x+y}{xy}\cdot\dfrac{xy}{x-y}=\dfrac{x+y}{x-y}\)

b:

ĐKXĐ: \(x\notin\left\{0;1;-1\right\}\)

 \(\dfrac{\dfrac{x}{x+1}-\dfrac{x-1}{x}}{\dfrac{x}{x-1}-\dfrac{x+1}{x}}\)

\(=\left(\dfrac{x^2-\left(x-1\right)\left(x+1\right)}{x\left(x+1\right)}\right):\dfrac{x^2-\left(x-1\right)\left(x+1\right)}{x\left(x-1\right)}\)

\(=\dfrac{x^2-x^2+1}{x\cdot\left(x+1\right)}\cdot\dfrac{x\left(x-1\right)}{x^2-x^2+1}\)

\(=\dfrac{x-1}{x+1}\)

c:

ĐKXĐ: \(x\ne-1\)

 \(1-\dfrac{x}{1-\dfrac{x}{x+1}}\)

\(=1-\dfrac{x}{\dfrac{x+1-x}{x+1}}\)

\(=1-\dfrac{x}{\dfrac{1}{x+1}}\)

\(=1-x\left(x+1\right)=1-x^2-x\)

\(B=\dfrac{-\left(2x^2+3\right)+2x^2+x+5}{2x^2+3}=-1+\dfrac{2\left(x+\dfrac{1}{4}\right)^2+\dfrac{39}{8}}{2x^2+3}>-1\)

\(B=\dfrac{2x^2+3-2x^2+x-1}{2x^2+3}=1-\dfrac{2\left(x-\dfrac{1}{4}\right)^2+\dfrac{7}{8}}{2x^2+3}< 1\)

\(\Rightarrow-1< B< 1\)

Mà B nguyên \(\Rightarrow B=0\)

\(\Rightarrow x+2=0\Rightarrow x=-2\)

a ) không tán thành.

b)tán thành 

\(P=\dfrac{3\left(x^2+1\right)}{3\left(x^2-x+1\right)}=\dfrac{2\left(x^2-x+1\right)+x^2+2x+1}{3\left(x^2-x+1\right)}=\dfrac{2}{3}+\dfrac{\left(x+1\right)^2}{3\left(x-\dfrac{1}{2}\right)^2+\dfrac{9}{4}}\ge\dfrac{2}{3}\)

\(P=\dfrac{2\left(x^2-x+1\right)-x^2+2x-1}{x^2-x+1}=2-\dfrac{\left(x-1\right)^2}{\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}}\le2\)

\(\Rightarrow\dfrac{2}{3}\le P\le2\)

Mà P nguyên \(\Rightarrow\left[{}\begin{matrix}P=1\\P=2\end{matrix}\right.\)

- Với \(P=1\Rightarrow\dfrac{x^2+1}{x^2-x+1}=1\Rightarrow x^2+1=x^2-x+1\)

\(\Rightarrow x=0\)

- Với \(P=2\Rightarrow\dfrac{x^2+1}{x^2-x+1}=2\Rightarrow x^2+x=2\left(x^2-x+1\right)\)

\(\Rightarrow x^2-2x+1=0\Rightarrow x=1\)

Vậy \(x=\left\{0;1\right\}\)

1: \(\dfrac{DM}{DE}=\dfrac{2}{5}\)

\(\dfrac{DN}{DF}=\dfrac{6}{15}=\dfrac{2}{5}\)

Do đó: \(\dfrac{DM}{DE}=\dfrac{DN}{DF}\)

2: Xét ΔDEF có \(\dfrac{DM}{DE}=\dfrac{DN}{DF}\)

nên MN//EF

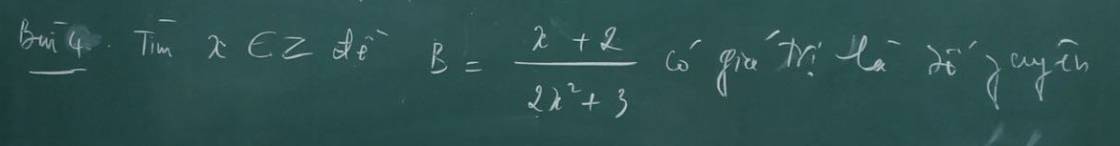
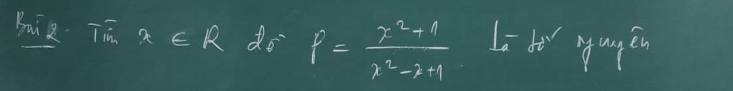
mày tự làm đi hỏi nhiều

advice nhé