Dế mèn phưu lưu kí là mộ câu chuyện rất hay do nhà văn tô hoài tạo ra từ nhỏ dế mèn đã được mẹ xây hộ cho cái nhà . Rồi sau đó bị lũ trẻ bắt làm trò chơi . Dế mèn đã giả vờ bị ốm rồi rốn đi . Sau đó làm anh em kế nghĩa với dế trũi . Một hôm trũi bị bắt dế mèn bèn đi tìm . Mộ hôm nọ dế mèn bị mộ con chim bắt . Ngày hôm đó may mà trũi trở về nên dế mèn mới thoát nạn.

dài hơn đc ko ạ

1: Xét ΔPMN có AB//MN

nên \(\dfrac{AB}{MN}=\dfrac{PA}{PM}\)

=>\(\dfrac{AB}{MN}=\dfrac{3}{7}\)

mà MN-AB=8

nên \(MN=8:\left(7-3\right)\cdot7=8:4\cdot7=14\left(cm\right)\)

=>AB=14-8=6(cm)

2:

a: Xét ΔABD có AE là phân giác

nên \(\dfrac{BE}{ED}=\dfrac{BA}{AD}\)

Xét ΔBAC có BF là phân giác

nên \(\dfrac{FA}{FC}=\dfrac{BA}{BC}=\dfrac{BA}{AD}\)

=>\(\dfrac{BE}{ED}=\dfrac{FA}{FC}\)

b:

Ta có: ABCD là hình bình hành

=>AC cắt BD tại trung điểm của mỗi đường

=>O là trung điểm chung của AC và BD

 \(\dfrac{BE}{ED}=\dfrac{FA}{FC}\)

=>\(\dfrac{BE}{ED}+1=\dfrac{FA}{FC}+1\)

=>\(\dfrac{BD}{ED}=\dfrac{AC}{FC}\)

mà BD=2OD và AC=2OC

nên \(\dfrac{2OD}{ED}=\dfrac{2OC}{FC}\)

=>\(\dfrac{OD}{ED}=\dfrac{OC}{FC}\)

Xét ΔODC có \(\dfrac{OD}{ED}=\dfrac{OC}{FC}\)

nên EF//CD

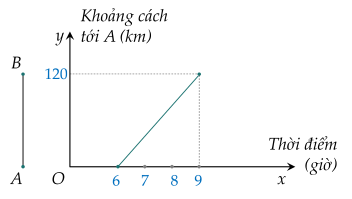
a: Đặt (d): y=ax+b 

Theo đồ thị, ta sẽ thấy: (d) đi qua A(6;0) và B(9;120)

Thay x=6 và y=0 vào y=ax+b, ta được:

\(a\cdot6+b=0\)

=>6a+b=0(1)

Thay x=9 và y=120 vào y=ax+b, ta được:

\(a\cdot9+b=120\)

=>9a+b=120(2)

Từ (1) và (2) ta có hệ phương trình:

\(\left\{{}\begin{matrix}9a+b=120\\6a+b=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}9a+b-6a-b=120\\6a+b=0\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}3a=120\\b=-6a\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=40\\b=-240\end{matrix}\right.\)

b: a=40; b=-240

=>y=40x-240

Thay x=8 vào y=40x-240, ta được:

\(y=40\cdot8-240=80\left(km\right)\)

=>Ô tô còn cách B 120-80=40km

a: Vì đường thẳng y=ax+b song song với đường thẳng y=3x-7 nên \(\left\{{}\begin{matrix}a=3\\b\ne-7\end{matrix}\right.\)

=>y=3x+b

Thay x=1 và y=2 vào y=3x+b, ta được:

\(b+3\cdot1=2\)

=>b+3=2

=>b=-1

Vậy: y=3x-1

b: Tọa độ giao điểm của (d1) và (d2) là:

\(\left\{{}\begin{matrix}2x-7=-3x+3\\y=2x-7\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}5x=10\\y=2x-7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=2\cdot2-7=-3\end{matrix}\right.\)

Thay x=2 và y=-3 vào y=ax+b, ta được:

\(a\cdot2+b=-3\)

=>2a+b=-3(1)

Thay x=-2 và y=5 vào y=ax+b, ta được:

\(a\cdot\left(-2\right)+b=5\)

=>-2a+b=5(2)

Từ (1) và (2) ta có hệ phương trình:

\(\left\{{}\begin{matrix}2a+b=-3\\-2a+b=5\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}2a+b-2a+b=-3+5\\2a+b=-3\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}2b=2\\2a=-3-b\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}b=1\\2a=-3-1=-4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-2\\b=1\end{matrix}\right.\)

a: 

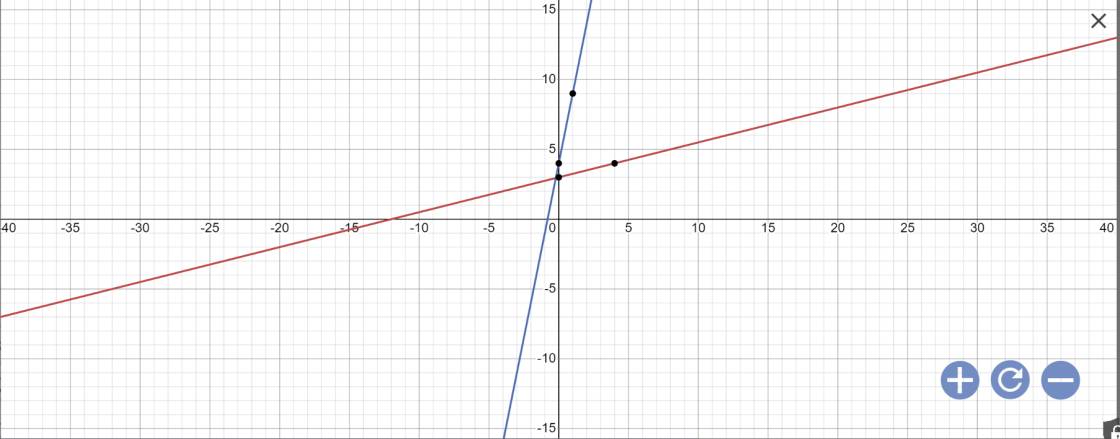
b: Tọa độ giao điểm của d1 với trục Ox là:

\(\left\{{}\begin{matrix}y=0\\\dfrac{1}{4}x+3=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\\dfrac{x}{4}=-3\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}x=-12\\y=0\end{matrix}\right.\)

Vậy: (d1) giao Ox tại A(-12;0)

Tọa độ giao điểm của (d1) với trục Oy là:

\(\left\{{}\begin{matrix}x=0\\y=\dfrac{1}{4}x+3=\dfrac{1}{4}\cdot0+3=3\end{matrix}\right.\)

vậy: (d1) giao Oy tại B(0;3)

Hãy viết bài văn phân tích một tác phẩm thơ trào phúng mà em tâm đắc nhất.