Khảo sát sự biến thiên và vẽ đồ thị của các hàm số sau:
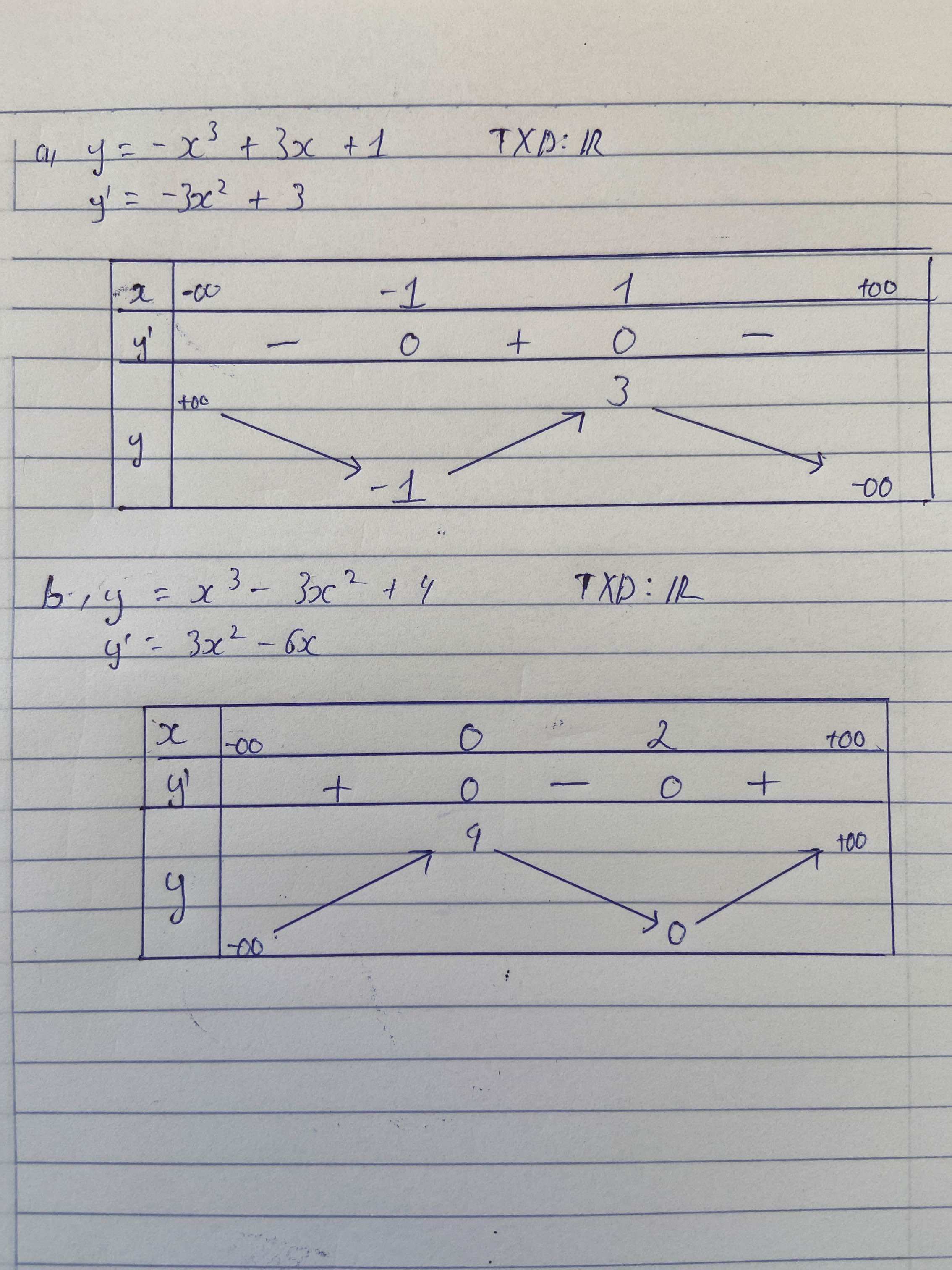
$a)$ $y=-x^3+3x+1;$
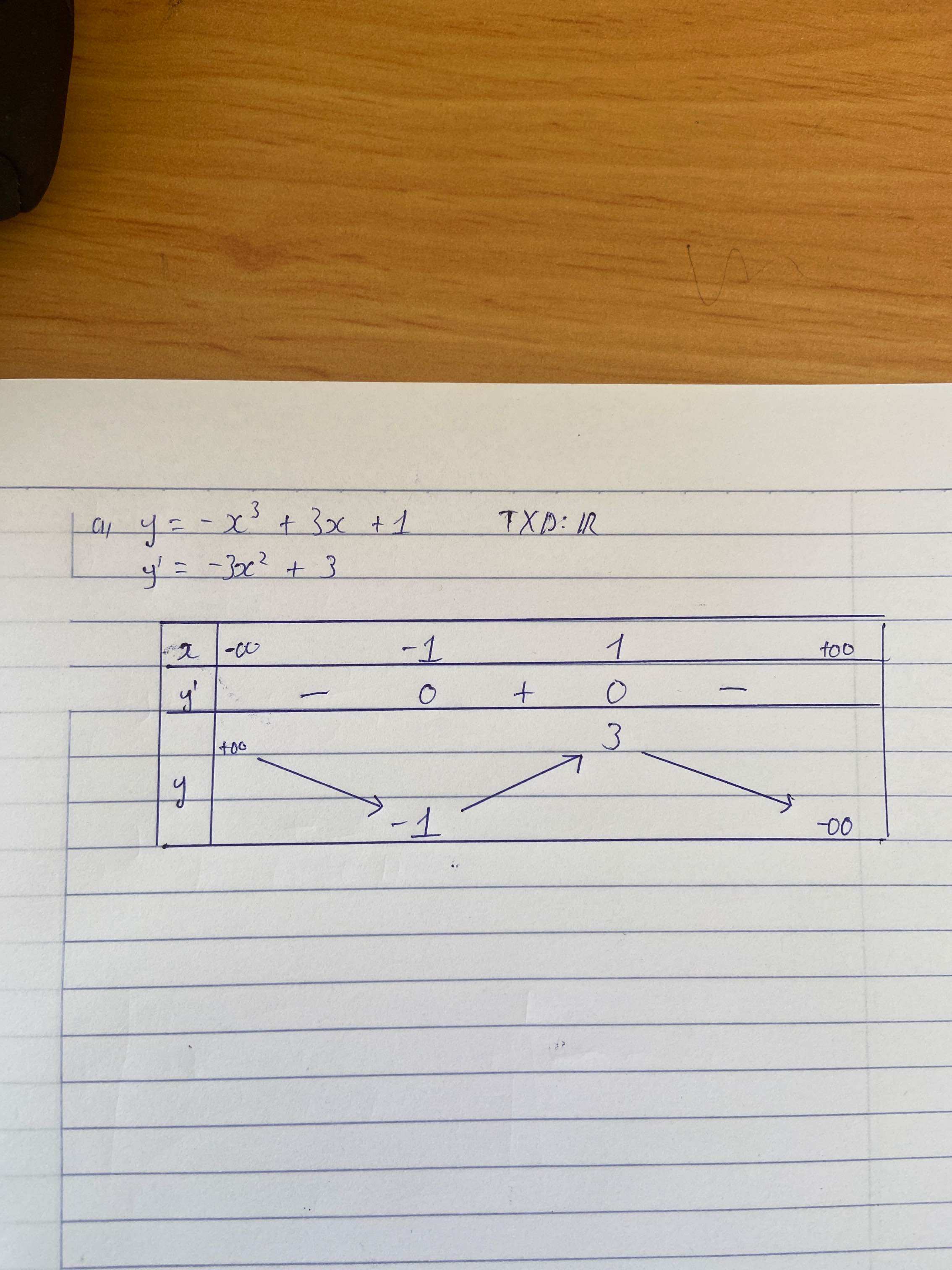
$b)$ $y=x^3 - 3x^2 + 4.$
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Khảo sát sự biến thiên và vẽ đồ thị của các hàm số sau:
$a)$ $y=-x^3+3x+1;$
$b)$ $y=x^3 - 3x^2 + 4.$





64.
d qua \(M\left(-3;1;2\right)\) và có vtcp \(\left(2;4;-1\right)\) nên có pt:
\(\left\{{}\begin{matrix}x=-3+2t\\y=1+4t\\z=2-t\end{matrix}\right.\)
C đúng
65.
\(\overrightarrow{AB}=\left(1;0;2\right)\) nên C đúng
66.
d qua \(M\left(3;-2;-6\right)\)
67.
mp vuông góc d nên nhận \(\left(1;2;-2\right)\) là 1 vtpt
Phương trình:
\(1\left(x-3\right)+2\left(y+2\right)-2\left(z-2\right)=0\)
\(\Leftrightarrow x+2y-2z+5=0\)
68.
M là giao d và (P) nên tọa độ thỏa mãn:
\(\left(-3+2t\right)+2\left(-1+t\right)-\left(3+t\right)+5=0\)
\(\Rightarrow t=1\)
Thay vào pt d:
\(\Rightarrow M\left(-1;0;4\right)\)
69.
\(\overrightarrow{BC}=\left(1;2;-1\right)\)
Đường thẳng đi qua A và song song BC nhận (1;2;-1) là 1 vtcp nên có pt:
\(\dfrac{x-1}{1}=\dfrac{y-2}{2}=\dfrac{z}{-1}\)

Trên \(\left[0;3\right]\) hàm \(y=x^2-3x\) âm nên ta cần "xoay" nó lên thành \(y=3x-x^2\)
Khi đó:
Pt hoành độ giao điểm trên \(\left[0;3\right]\): \(3x-x^2=x\Rightarrow\left[{}\begin{matrix}x=0\\x=2\end{matrix}\right.\)
Pt hoành độ giao điểm với \(x>3\): \(x^2-3x=x\Rightarrow x=4\)
Do đó:
\(V=\pi\int\limits^2_0\left(3x-x^2\right)^2dx+\pi\int\limits^4_2x^2dx-\pi\int\limits^4_3\left(x^2-3x\right)^2dx=\dfrac{611\pi}{30}\)
\(\Rightarrow18a-300b=1998\)


\(\overrightarrow{BA}=\left(1;1;2\right)\)
Pt AB có dạng: \(\left\{{}\begin{matrix}x=-2+t\\y=1+t\\z=1+2t\end{matrix}\right.\)
Pt mặt phẳng qua C và vuông góc AB có dạng:
\(1\left(x-5\right)+y+2z=0\)
\(\Leftrightarrow x+y+2z-5=0\)
Tọa độ H thỏa mãn:
\(\left(-2+t\right)+\left(1+t\right)+2\left(1+2t\right)-5=0\)
\(\Rightarrow t=\dfrac{2}{3}\Rightarrow H\left(-\dfrac{4}{3};\dfrac{5}{3};\dfrac{7}{3}\right)\)

Olm chào em, cảm ơn em đã lựa chọn gói vip của Olm, cảm ơn đánh giá của em về chất lượng bài giảng, bài học của Olm.
Chúc em học tập vui vẻ và hiệu quả cùng Olm.vn