Hai dây dẫn kim loại cùng chất, có cùng chiều dài nhưng tiết diện khác nhau (tiết diện dây thứ nhất lớn hơn) được mắc nối tiếp vào một nguồn điện. So sánh hiệu điện thế trên hai dây.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Áp dụng định lý cosin cho tam giác ABC, ta được:
\(BC=\sqrt{AB^2+AC^2-2AB.AC.cosA}\)
\(=\sqrt{21^2+16^2-2.21.16.cos60^o}\)
\(=19\)
Do đó \(p=\dfrac{AB+BC+CA}{2}=\dfrac{21+16+19}{2}=28\)
Mà \(S_{ABC}=\dfrac{1}{2}AB.AC.sinA=\dfrac{1}{2}.21.16.sin60^o=84\sqrt{3}\)
Mặt khác, \(S_{ABC}=pr=28r\) (\(r\) là bán kính đường tròn nội tiếp \(\Delta ABC\))
\(\Rightarrow28r=84\sqrt{3}\Leftrightarrow r=3\sqrt{3}\)

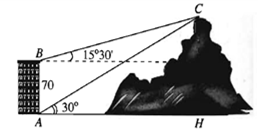
ˆABC=90°+15°30'=105°30'
Xét tam giác ABC có ˆCAB =60°, ˆABC=105°30' ta có:
ˆCAB+ˆABC+ˆACB=180° (định lí tổng ba góc trong tam giác)
⇒ˆACB=180°−ˆCAB−ˆABC
⇒ˆACB=180°−60°−105°30'=14°30'.
Áp dụng định lí sin trong tam giác ABC, ta có: ACsinˆABC=ABsinˆACB
⇒AC=AB.sinˆABCsinˆACB=70.sin105°30'sin14°30'≈269,4(m)

1.Ta có: ABCDABCD là hình vuông
→→CB=→DA→CB→=DA→
→→OA−→CB=→OA−→DA=→OA+→AD=→OD→OA→−CB→=OA→−DA→=OA→+AD→=OD→
→|→OA−→CB|=|→OD|=OD=a√2→|OA→−CB→|=|OD→|=OD=a2
2.Ta có:
→DA−→DB+→DCDA→−DB→+DC→
=→BA+→DC=BA→+DC→
=→BA−→CD=BA→−CD→
=→BA−→BA=BA→−BA→ vì ABCDABCD là hình vuông
→CD=→BA→CD→=BA→
=0⃗

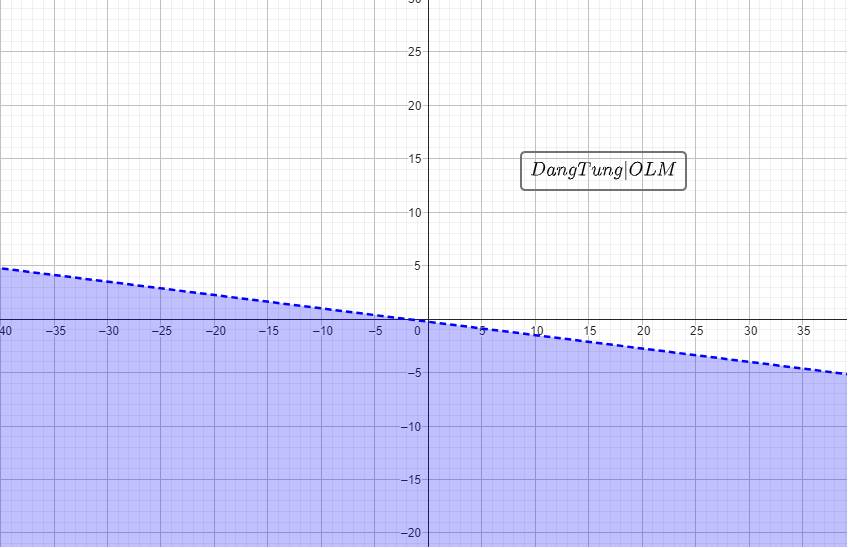
\(\dfrac{x-2y}{2}>\dfrac{2x+y+1}{3}\\ < =>3\left(x-2y\right)>2\left(2x+y+1\right)\\ < =>3x-6y>4x+2y+2\\ < =>4x-3x+2y+6y< -2\\ < =>x+8y< -2\)





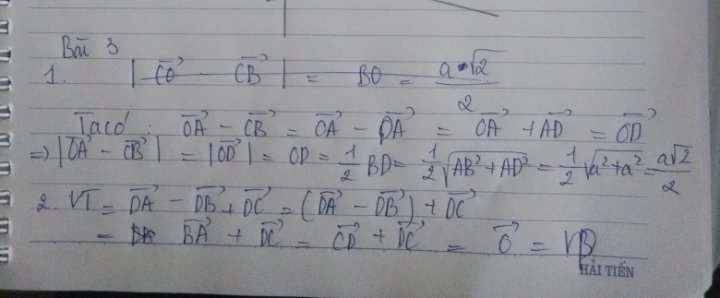


Vì \(S_1>S_2\Rightarrow R_1< R_2\Rightarrow U_2< U_1 \)