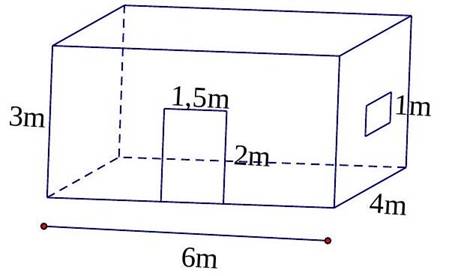
Bài 8. Căn phòng của anh An có hình hộp chữ nhật với chiều dài , chiều rộng , chiều cao . Phòng có một của lớn hình chữ nhật và một của sổ hình vuông cạnh (như hình vẽ). Anh
An muốn sơn bốn bức tường bên trong căn phòng này (không sơn cửa). Hỏi diện tích anh An cần sơn là bao nhiêu?