cho tam giác ABC và I là giao điểm của 3 đường phân giác. Gọi H là chân đường vuông góc kẻ từ B đến AI. Chứng minh IBH=ICA
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


DG
23 tháng 5 2020
jfccfffcfffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffff

24 tháng 5 2020
 (mạng cx đã có phần gợi ý, vc còn lại là lắp vào bài thôi.)
(mạng cx đã có phần gợi ý, vc còn lại là lắp vào bài thôi.)
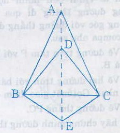
Xét \(\Delta\)ABC cân tại A ta có :
AB = AC
=> A thuộc đường trung trức của BC (1)
Xét \(\Delta\)DBC cân tại D ta có
DB = DC
=> D thuộc đường trung trực của BC (2)
Xét \(\Delta\)EBC cân tại E ta có :
EB = EC
=> E thuộc đường trung trực của BC (3)
Từ (1) ; (2) và (3)
Suy ra : A ; D ; E thuộc đường trung trực BC
và A ; D ; E thẳng hàng
Nguồn (gợi ý): Bài 46 SGK - tập 2 trang 76 - Toán lớp 7 | Học trực tuyến (vào TK nhìn thấy)
Vì BI và CI là phân giác => AI cũng là phân giác
Ta có \(\widehat{\text{BAI}}=\widehat{CAH}=\frac{\widehat{BAC}}{2}\) ( AI là phân giác)
\(\widehat{\text{ACI}}\)=\(\widehat{\text{BCI}}\)=\(\frac{\widehat{\text{ACB}}}{2}\)(CI là phân giác)
\(\widehat{\text{ABI}}=\)\(\widehat{\text{CBI}}=\)\(\widehat{\frac{\text{ABC}}{2}}\) (BI là phân giác)
Xét tam giác vuông \(AHB\Rightarrow\widehat{IAB}+\widehat{ABH}=90^0\)\(\text{AHB => IAB + ABH = 90}\)
\(\Rightarrow IAB+ABI+IBH=90^0\)
\(\Rightarrow IBH=90^0-\left(IAB+ABI\right)\left(1\right)\)
Xét \(\Delta ABC\) có \(\widehat{\text{BAC}}\)\(+\widehat{\text{ABC}}\)\(+\widehat{\text{ACB}}\)\(\text{= 180}^0\)
\(\Rightarrow\frac{\left(\widehat{BAC}+\widehat{ABC}+\widehat{ACB}\right)}{2}=\frac{180^0}{2}=90^0\)
\(\frac{\widehat{BAC}}{2}+\widehat{\frac{ABC}{2}}+\frac{\widehat{ACB}}{2}=90^0\)
Lại có \(\widehat{\text{BAI}}\) \(=\widehat{\text{CAH}}\) \(=\frac{\widehat{BAC}}{2}\) \(;\widehat{\text{ABI}}\)\(=\widehat{\text{CBI}}=\)\(\frac{\widehat{\text{ABC}}}{2}\) và \(\widehat{\text{ABI}}=\)\(\widehat{\text{CBI}}\)\(=\widehat{\frac{\text{ABC}}{2}}\)
\(\Rightarrow\) \(\widehat{\text{IAB}}\) +\(\widehat{\text{ ABI}}\) + \(\widehat{\text{ACI}}=90^0\)
\(\Rightarrow\widehat{\text{ACI }}=90^0-\left(\widehat{IAB}+\widehat{ABH}\right)\left(2\right)\)
Từ (1) và (2) => \(\widehat{\text{IBH}}=\widehat{ACI}\)
A B H C I