Cần số khoang là: 818 : 4 = 204,5 (khoang)

Cần số toa tàu là: 204,5 : 10 = 20,45 (toa)

Số hơi lẻ nên mình cũng không chắc lắm

Diện tích cái ao bằng - là sao em?

dạ em quên diện tích ao bằng 3/7 diện tích trồng hoa...

Lời giải:
$\frac{2010\times 125+1010}{126\times 1010-1000}$

$=\frac{252260}{126260}=\frac{12613}{6313}$

Lời giải:

$\frac{45\times 16-17}{45\times 15+28}=\frac{45\times (15+1)-17}{45\times 15+28}$

$=\frac{45\times 15+28}{45\times 15+28}=1$

1 nha

1 nha bạn

Có phải là tính giá trị của biểu thức không em?

Nếu đúng thì làm như sau em nhé:

    28 + 62  x a x (a x 1 - a : 1) + 28 x 8 + 28

= 28 + 62 x a x (a - a) + 28 x 8 + 28

= 28 x 1  + 62 x a x 0 + 28 x 9 + 28 x 1

= 28 x 1 + 0 + 28 x 8 + 28 x 1

= 28 x ( 1 + 8 + 1)

=  28 x 10

= 280

Đề yêu cầu gì em nhỉ?

     Đây là dạng toán nâng cao chuyên đề toán hai tỉ số, cấu trúc thi chuyên thi học sinh giỏi các cấp, thi violympic. Hôm nay, Olm sẽ hướng dẫn các em giải chi tiết dạng này bằng sơ đồ như sau:

                          Giải:

\(\dfrac{3}{5}\) số thứ nhất và \(\dfrac{3}{5}\) số thứ hai là: 140 x \(\dfrac{3}{5}\) = 84 

Theo bài ra ta có sơ đồ:

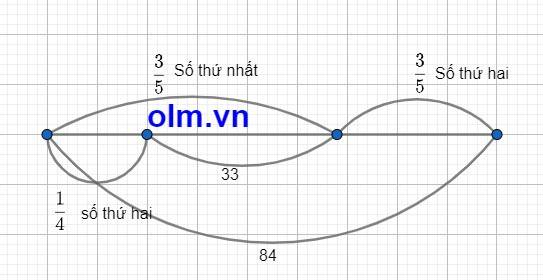
Theo sơ đồ ta có:

\(\dfrac{1}{4}\) số thứ hai  và \(\dfrac{3}{5}\) số thứ hai là: 84 - 33 = 51

51 ứng với: \(\dfrac{1}{4}\) + \(\dfrac{3}{5}\) = \(\dfrac{17}{20}\) (số thứ hai)

Số thứ hai là: 51 : \(\dfrac{17}{20}\) = 60

Số thứ nhất là: 140 -  60 = 80

Đáp số: số thứ nhất 80

             số thứ hai 60

Lời giải:
Gọi số thứ nhất là $a$ và số thứ hai là $b$. Theo bài ra ta có:

$a+b=140$

$a=140-b$

$\frac{3}{5}\times a-\frac{1}{4}\times b=33$

Thay $a=140-b$ vào điều kiện trên thì:

$\frac{3}{5}\times (140-b)-\frac{1}{4}\times b=33$

$84-\frac{3}{5}\times b-\frac{1}{4}\times b=33$

$84-b\times (\frac{3}{5}+\frac{1}{4})=33$

$84-b\times \frac{17}{20}=33$
$b\times \frac{17}{20}=84-33=51$

$b=51:\frac{17}{20}=60$

$a=140-b=140-60=80$

Vậy hai số cần tìm là $80$ và $60$

Nước muối.

nước muối nha bạn

Lời giải:

a. Áp dụng định lý Pitago:

$AC=\sqrt{BC^2-AB^2}=\sqrt{10^2-6^2}=8$ 

$AH=2S_{ABC}:BC=AB.AC:BC=6.8:10=4,8$ 

b.

Xét tam giác $AEH$ và $AHB$ có:

$\widehat{A}$ chung

$\widehat{AEH}=\widehat{AHB}=90^0$

$\Rightarrow \triangle AEH\sim \triangle AHB$ (g.g)

$\Rightarrow \frac{AE}{AH}=\frac{AH}{AB}$

$\Rightarrow AH^2=AE.AB(1)$
Hoàn toàn tương tự: $\triangle AFH\sim \triangle AHC$

$\Rightarrow AH^2=AF.AC(2)$

Từ $(1); (2)\Rightarrow AE.AB=AF.AC$

c.

$HE\perp AB, AB\perp AC$ nên $HE\parallel AC$

Tam giác vuông $BEH$ vuông tại $E$ có trung tuyến $EM$ ứng với cạnh huyền $BH$

nên $EM=\frac{BH}{2}=MH$

$\Rightarrow EMH$ cân tại $M$

$\Rightarrow \widehat{MEH}=\widehat{MHE}=\widehat{HCA}(3)$ (2 góc đồng vị)

Tứ giác $AEHF$ có 3 góc $\widehat{A}=\widehat{E}=\widehat{F}=90^0$ nên là hcn. 

$\Rightarrow \widehat{HEF}=\widehat{HAF}=\widehat{HAC}(4)$

Từ $(3); (4)\Rightarrow \widehat{MEH}+\widehat{HEF}=\widehat{HCA}+\widehat{HAC}$

$\Rightarrow \widehat{MEF}=\widehat{HCA}+\widehat{HAC}=90^0$

$\Rightarrow EM\perp EF$

Hình vẽ:

Where did you go yesterday afternoon?

          TICK NHA~

What did we do yesterday afternoon?