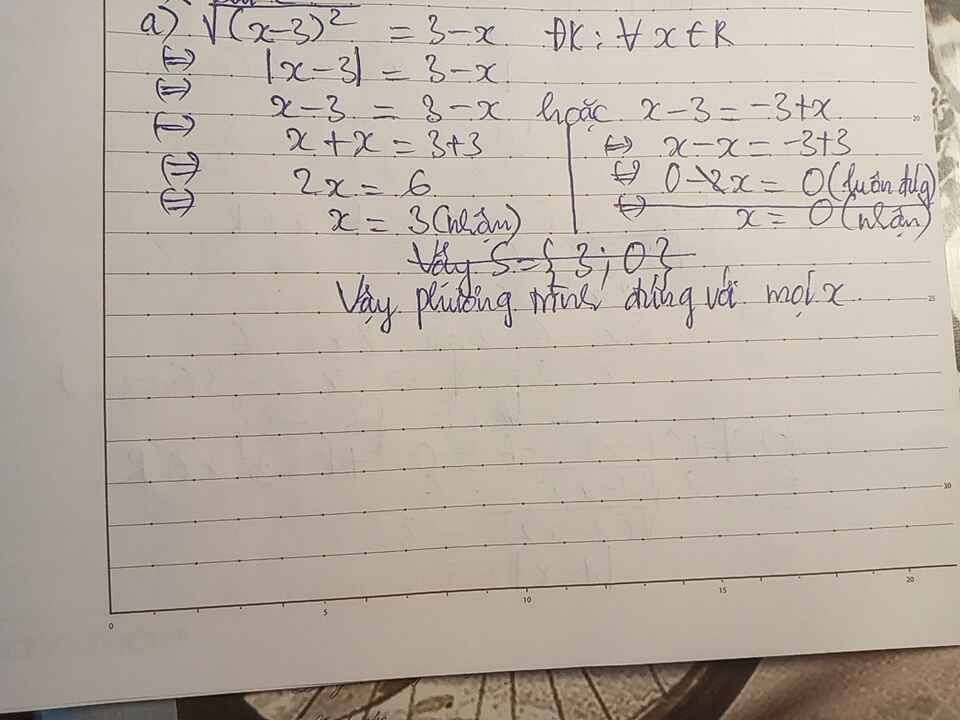
đkxđ: \(z\ge1;x\ge2;y\ge3\)

Đặt \(a=\sqrt{z-1}\ge0;b=\sqrt{x-2}\ge0;c=\sqrt{y-3}\ge0\)

\(\Rightarrow z=a^2+1;x=b^2+2;y=c^2+3\)

\(\Rightarrow A=\dfrac{a}{a^2+1}+\dfrac{b}{b^2+2}+\dfrac{c}{c^2+3}\)

Do các biến \(a,b,c\) độc lập nhau nên ta xét từng phân thức một.

Đặt \(f\left(a\right)=\dfrac{a}{a^2+1}\) \(\Rightarrow f\left(a\right).a^2-a+f\left(a\right)=0\) (*)

Nếu \(f\left(a\right)=0\) thì \(a=0\), rõ ràng đây không phải là GTLN cần tìm.

Xét \(f\left(a\right)\ne0\)

Để pt (*) có nghiệm thì \(\Delta=\left(-1\right)^2-4\left[f\left(a\right)\right]^2\ge0\) 

\(\Leftrightarrow\left(1+2f\left(a\right)\right)\left(1-2f\left(a\right)\right)\ge0\)

\(\Leftrightarrow-\dfrac{1}{2}\le f\left(a\right)\le\dfrac{1}{2}\)

\(f\left(a\right)=\dfrac{1}{2}\Leftrightarrow\dfrac{a}{a^2+1}=\dfrac{1}{2}\Leftrightarrow a^2+1=2a\Leftrightarrow a=1\) (nhận)

Vậy \(max_{f\left(a\right)}=\dfrac{1}{2}\).

 Tiếp đến, gọi \(g\left(b\right)=\dfrac{b}{b^2+2}\) \(\Rightarrow g\left(b\right).b^2-b+2g\left(b\right)=0\) (**)

 Tương tự nếu \(b=0\) thì vô lí. Xét \(b\ne0\). Khi đó để (**) có nghiệm thì \(\Delta=\left(-1\right)^2-8\left[g\left(b\right)\right]^2\ge0\)

\(\Leftrightarrow\left(1-2\sqrt{2}g\left(b\right)\right)\left(1+2\sqrt{2}g\left(b\right)\right)\ge0\)

\(\Leftrightarrow-\dfrac{1}{2\sqrt{2}}\le g\left(b\right)\le\dfrac{1}{2\sqrt{2}}\)

\(g\left(b\right)=\dfrac{1}{2\sqrt{2}}\Leftrightarrow\dfrac{b}{b^2+2}=\dfrac{1}{2\sqrt{2}}\Leftrightarrow b^2+2=2\sqrt{2}b\Leftrightarrow b=\sqrt{2}\) (nhận)

Vậy \(max_{g\left(b\right)}=\dfrac{1}{2\sqrt{2}}\)

Làm tương tự với \(h\left(c\right)=\dfrac{c}{c^2+3}\), ta được \(max_{h\left(c\right)}=\dfrac{1}{2\sqrt{3}}\), xảy ra khi \(c=\sqrt{3}\)

Vậy GTLN của A là \(\dfrac{1}{2}+\dfrac{1}{2\sqrt{2}}+\dfrac{1}{2\sqrt{3}}=\dfrac{6+3\sqrt{2}+2\sqrt{3}}{12}\), xảy ra khi \(\left(a,b,c\right)=\left(1,\sqrt{2},\sqrt{3}\right)\) hay \(\left(x,y,z\right)=\left(2,4,6\right)\).

Cái chỗ cuối mình sửa thế này nhé

C

c

XX được gọi là cặp tương đồng

XY được gọi là cặp không tương đồng 

vẽ trên phần mềm Paint nha bạn

Bài làm của bạn chưa đúng nhé:

Đến đoạn

$|x-3|=3-x$

$\Leftrightarrow |3-x|=3-x$
$\Leftrightarrow 3-x\geq 0$

$\Leftrightarrow x\leq 3$

Vậy pt có nghiệm $x\leq 3, x\in\mathbb{R}$

----------------------------

Bạn nhớ 1 tính chất này: Nếu $|a|=a$ thì $a\geq 0$.

\(\dfrac{x+2\sqrt{x}}{\sqrt{x}-1}=8\left(x\ge0;x\ne1\right)\)

\(\Leftrightarrow x+2\sqrt{x}=8\left(\sqrt{x}-1\right)\)

\(\Leftrightarrow x+2\sqrt{x}=8\sqrt{x}-8\)

\(\Leftrightarrow x+2\sqrt{x}-8\sqrt{x}+8=0\)

\(\Leftrightarrow x-6\sqrt{x}+8=0\)

\(\Leftrightarrow\left(\sqrt{x}-4\right)\left(\sqrt{x}-2\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x}-2=0\\\sqrt{x}-4=0\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x}=2\\\sqrt{x}=4\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=4\\x=16\end{matrix}\right.\left(tm\right)\)

Vậy: ... 

\(\dfrac{x+2\sqrt{x}}{\sqrt{x}-1}=8\left(x\ge0,x\ne1\right)\\ < =>x+2\sqrt{x}=8\sqrt{x}-8\\ < =>x-6\sqrt{x}+8=0\\ < =>\left(\sqrt{x}-2\right)\left(\sqrt{x}-4\right)=0\\ =>\left[{}\begin{matrix}\sqrt{x}-2=0\\\sqrt{x}-4=0\end{matrix}\right.\\ < =>\left[{}\begin{matrix}x=4\\x=16\end{matrix}\right.\left(TMDK\right)\)

\(=>S=\left\{4;16\right\}\)

CTM: \(R_1ntR_2\)

\(R_{tđ}=R_1+R_2\), mà \(R_2=3R_1\) nên:

\(R_{tđ}=R_1+3R_1=4R_1=17\) \(\Rightarrow R_1=\dfrac{17}{4}\Omega=4,25\Omega\)

\(\Rightarrow R_2=3R_1=3\cdot4,25=12,75\Omega\)

ctm là j bạn