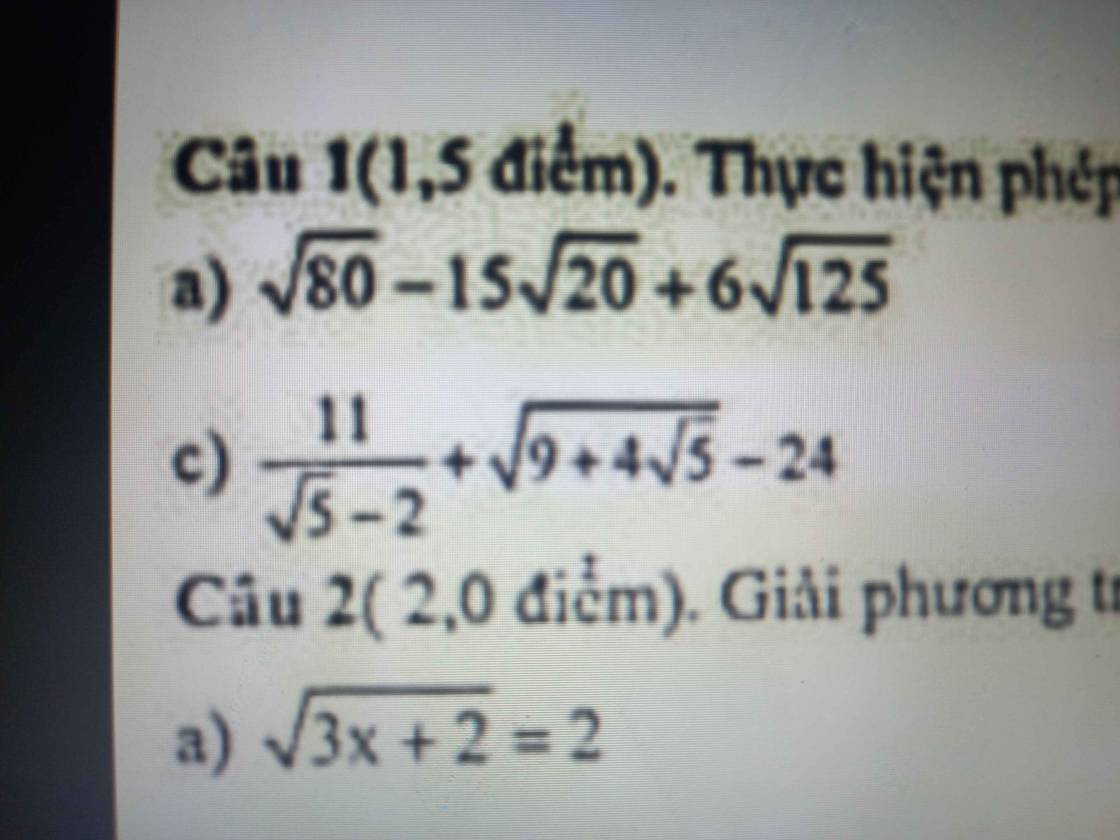a.Ta có:
$\widehat{AKC}=\widehat{AHB}={90}^o,\widehat{KAC}=\widehat{BAH}$

$\to \Delta AKC\sim \Delta AHB(g.g)$

$\to \frac{AK}{AH}=\frac{AC}{AB}$

$\to \frac{AK}{AC}=\frac{AH}{AB}$

Mà $\widehat{KAH}=\widehat{BAC}$

$\to \Delta AKH\sim \Delta ACB(c.g.c)$

$\to \frac{KH}{BC}=\frac{AK}{AC}=\cos \widehat{KAC}=\cos A$

$\to HK=BC.\cos A$ 

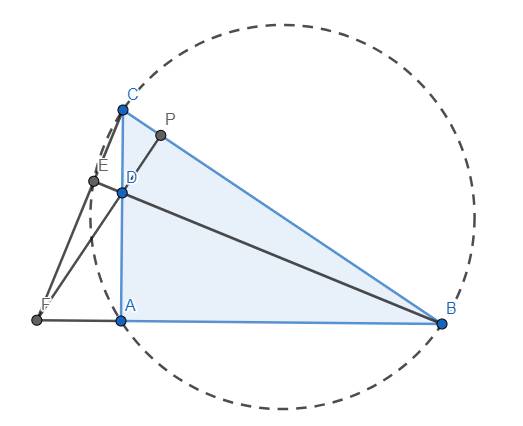
 a) Ta có \(\widehat{CEB}=\widehat{CAB}=90^o\) nên 4 điểm A, B, C, E cùng thuộc đường tròn đường kính BC.

 b) Kẻ \(FP\perp BC\) tại P. Ta thấy D là trực tâm tam giác FBC nên \(P\in DF\). Dễ thấy \(\Delta CDP~\Delta CBA\left(g.g\right)\) \(\Rightarrow\dfrac{CD}{CB}=\dfrac{CP}{CA}\) \(\Rightarrow CD.CA=CB.CP\)

CMTT, ta có \(BD.BE=BC.BP\)

Do đó \(CD.CA+BD.BE=CB.CP+BC.BP\) \(=BC\left(CP+BP\right)\) \(=BC^2\). Vậy đẳng thức được chứng minh.

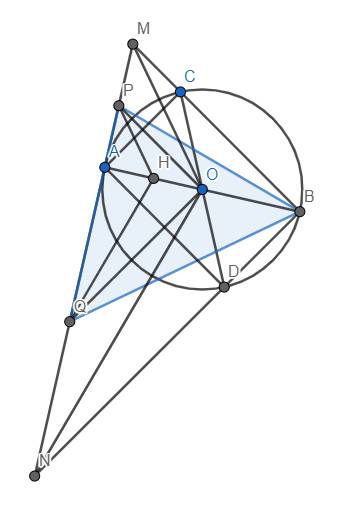
 a) Tam giác ABM vuông tại A có đường cao AC nên \(BC.BM=BA^2\). CMTT, \(BD.BN=BA^2\) nên \(BC.BM=BD.BN\Leftrightarrow\dfrac{BM}{BD}=\dfrac{BN}{BC}\). Từ đây dễ dàng suy ra \(\Delta BNM~\Delta BCD\left(c.g.c\right)\) (đpcm)

 b) Ta có OQ//BN, OP//BM, mà \(MB\perp NB\) nên suy ra \(OP\perp BN\), từ đó O là trực tâm tam giác BPN.\(\Rightarrow ON\perp BP\)

 Lại có \(QH\perp BP\) nên QH//ON.

Tam giác AON có Q là trung điểm AN, QH//ON nên H là trung điểm OA \(\Rightarrow AH=\dfrac{OA}{2}=\dfrac{R}{2}\) không đổi.

 Tóm tắt :

        Biết : $R_1=3\Omega$ ; $R_2=5\Omega$ ; $R_3=7\Omega$

                  $U=6V$

        Tính : a. $R_{tđ}=?$

                  b. $U_1=?$ ; $U_2=?$ ; $U_3=?$ 

                                                  Giải

b.   CĐDĐ qua mạch chính là :

           $I=\frac{U}{R}=\frac{6}{15}=0,4A$

       Do $R_1$ nt $R_2$ nt $R_3$ nên :

          $I=I_1=I_2=I_3=0,4A$

       HĐT giữa hai đầu mỗi điện trở là :

             $U_1=I_1.R_1=0,4.3=1,2V$

             $U_2=I_2.R_2=0,4.5=2V$

             $U_3=I_3.R_3=0,4.7=2,8V$

                      Đáp số  $U_1=1,2V$ ; $U_2=2V$ ; $U_3=2,8V$

ko bit đúng ko nũa

help me các bạn giúp m với