Tìm m để phương trình : x²-2x-mx+2m=0 có 2 nghiệm phân biệt
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Giải:
Gọi chiều rộng của mảnh đất hình chữ nhật là: \(x\) (m); \(x\) > 0
Chiều dài của mảnh đất hình chữ nhật là: \(x\) x 2 = 2\(x\) (m)
Chiều dài của cái ao là: 2\(x\) - 1 x 2 = 2\(x\) - 2 (m)
Chiều rộng của cái ao là: \(x\) - 1 x 2 = \(x\) - 2 (m)
Diện tích của cái ao là: (2\(x\) - 2) x (\(x\) - 2)
Theo bài ra ta có phương trình:
(2\(x\) - 2) x (\(x-2\)) = 60
2\(x^2\) - 4\(x\) - 2\(x\) + 4 = 60
2\(x^2\) - (4\(x\) + 2\(x\)) + 4 = 60
2\(x^2\) - 6\(x\) + 4 - 60 = 0
2\(x^2\) - 6\(x\) - 56 = 0
\(\Delta^,\) = 32 - (- 56)x 2 = 121 > 0
Vậy phương trình có hai nghiệm lần lượt là:
\(x_1\) = (3 + \(\sqrt{121}\)) : 2 = 7
\(x_2\) = (3 - \(\sqrt{121}\)): 2 = - 4 < 0 (loại)
Vậy \(x\) = 7
Chiều rộng của mảnh đất là: 7m
Chiều dài của mảnh đất là: 7 x 2 = 14 (m)
Kết luận các kích thước của mảnh đất là chiều rộng 7m; chiều dài 14m

Bạn nên gõ đề bằng công thức toán (biểu tượng $\sum$ góc trái khung soạn thảo) để mọi người đọc hiểu đề và hỗ trợ bạn nhanh hơn nhé.

a, Với \(x\ge0;x\ne1\):
\(P=\left(\dfrac{\sqrt{x}-2}{x-1}-\dfrac{\sqrt{x}+2}{x+2\sqrt{x}+1}\right).\dfrac{\left(1-x\right)^2}{2}\)
\(=\left[\dfrac{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)^2}-\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+2\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)^2}\right].\dfrac{\left(x-1\right)^2}{2}\)
\(=\dfrac{x-\sqrt{x}-2-\left(x+\sqrt{x}-2\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)^2}.\dfrac{\left(\sqrt{x}-1\right)^2\left(\sqrt{x}+1\right)^2}{2}\)
\(=\dfrac{-2\sqrt{x}\left(\sqrt{x}-1\right)}{2}=\sqrt{x}\left(1-\sqrt{x}\right)=\sqrt{x}-x\)
b, Thay \(x=7-4\sqrt{3}\) vào P, ta được:
\(P=\sqrt{7-4\sqrt{3}}-\left(7-4\sqrt{3}\right)\)
\(=\sqrt{\left(\sqrt{3}\right)^2-2.\sqrt{3}.2+2^2}+4\sqrt{3}-7\)
\(=\sqrt{\left(\sqrt{3}-2\right)^2}+4\sqrt{3}-7\)
\(=\left|\sqrt{3}-2\right|+4\sqrt{3}-7\)
\(=2-\sqrt{3}+4\sqrt{3}-7\) (vì \(\sqrt{3}< 2\))
\(=-5+3\sqrt{3}\)
$Toru$
a) \(P=\left(\dfrac{\sqrt{x}-2}{x-1}-\dfrac{\sqrt{x}+2}{x+2\sqrt{x}+1}\right).\dfrac{\left(1-x\right)^2}{2}\left(x\ge0,x\ne1\right)\\ =\left[\dfrac{\sqrt{x}-2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}-\dfrac{\sqrt{x}+2}{\left(\sqrt{x}+1\right)^2}\right].\dfrac{\left(x-1\right)^2}{2}\\ =\dfrac{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)-\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}{\left(\sqrt{x}+1\right)^2\left(\sqrt{x}-1\right)}.\dfrac{\left(x-1\right)^2}{2}\\ \)
\(=\dfrac{x-2\sqrt{x}+\sqrt{x}-2-\left(x+2\sqrt{x}-\sqrt{x}-2\right)}{\left(x-1\right)\left(\sqrt{x}+1\right)}.\dfrac{\left(x-1\right)\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{2}\\ =\left[x-\sqrt{x}-2-\left(x+\sqrt{x}-2\right)\right].\dfrac{\sqrt{x}-1}{2}\\ \)
\(=-2\sqrt{x}.\dfrac{\sqrt{x}-1}{2}\\ =-\sqrt{x}\left(\sqrt{x}-1\right)=-x+\sqrt{x}\)
b) \(x=7-4\sqrt{3}\left(TMDK\right)\)
\(\sqrt{x}=\sqrt{\left(2-\sqrt{3}\right)^2}=\left|2-\sqrt{3}\right|=2-\sqrt{3}\)
Thay vào biểu thức P, ta được:
\(P=-\left(7-4\sqrt{3}\right)+2-\sqrt{3}=-5+3\sqrt{3}\)


- Trích mẫu thử.
- Hòa tan từng mẫu thử vào nước.
+ Tan: Na2O
PT: \(Na_2O+H_2O\rightarrow2NaOH\)
+ Không tan: CuO, Al2O3, MgO. (1)
- Cho mẫu thử nhóm (1) pư với HCl rồi nhỏ NaOH thu được ở thí nghiệm trên vào.
+ Có tủa xanh: CuO
PT: \(CuO+2HCl\rightarrow CuCl_2+H_2O\)
\(CuCl_2+2NaOH\rightarrow2NaCl+Cu\left(OH\right)_{2\downarrow}\)
+ Có tủa keo trắng rồi tan trong NaOH dư: Al2O3
PT: \(Al_2O_3+6HCl\rightarrow2AlCl_3+3H_2O\)
\(2AlCl_3+6NaOH\rightarrow2Al\left(OH\right)_{3\downarrow}+6NaCl\)
\(Al\left(OH\right)_3+NaOH\rightarrow NaAlO_2+2H_2O\)
+ Có tủa trắng: MgO
PT: \(MgO+2HCl\rightarrow MgCl_2+H_2O\)
\(MgCl_2+2NaOH\rightarrow NaCl+Mg\left(OH\right)_{2\downarrow}\)
- Dán nhãn.

Lời giải:
Áp dụng BĐT Bunhiacopxky:
$(\sqrt{2a+b}+\sqrt{2b+c}+\sqrt{2c+a})^2\leq [(2a+b)+(2b+c)+(2c+a)](1+1+1)=3(a+b+c).3=9(a+b+c)=81$
$\Rightarrow \sqrt{2a+b}+\sqrt{2b+c}+\sqrt{2c+a}\leq 9$
Vậy ta có đpcm
Dấu "=" xảy ra khi $a=b=c=3$
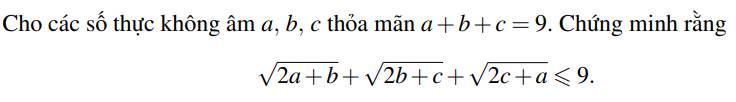
\(x^2-x\left(m+2\right)+2m=0\)
De pt co 2 nghiem phan biet khi delta > 0
\(\Delta=\left(m+2\right)^2-4.2m=m^2+4m+4-8m=m^2-4m+4=\left(m-2\right)^2\)
Ma (m-2)^2 >= 0 voi moi x
=> m - 2 \(\ne0\Rightarrow m\ne2\)
\(x^2-2x-mx+2m=0\)
\(x^2-\left(2+m\right)x+2m=0\)
\(\Delta=\left[-\left(2+m\right)\right]^2-4.1.2m\)
\(=4+4m+m^2-8m\)
\(=m^2-4m+4\)
\(=\left(m-2\right)^2\)
Để phương trình có hai nghiệm phân biệt thì \(\Delta>0\)
\(\left(m-2\right)^2>0\)
\(m-2\ne0\)
\(m\ne2\)
Vậy \(m\ne2\) thì phương trình đã cho có hai nghiệm phân biệt