a) \(3,2x-1,2x+2,7=-4,9\)

\(x\left(3,2-1,2\right)+2,7=-4,9\)

\(2x=-7,6\)

\(\Rightarrow x=-7,6\div2=-3,8\)

b) \(-\frac{1}{10}+\frac{2x}{5}+\frac{7}{20}=\frac{1}{10}\)

\(\frac{2x}{5}+\frac{1}{4}=\frac{1}{10}\)

\(\frac{2x}{5}=\frac{1}{10}-\frac{1}{4}\)

\(\frac{2x}{5}=-\frac{3}{20}\)

\(\Rightarrow2x=-\frac{3}{20}.5=-\frac{3}{4}\)

\(\Rightarrow x=-\frac{3}{4}\div2=-\frac{3}{8}\)

c) \(\frac{5}{7}+\frac{2x}{3}=\frac{3}{10}\)

\(\frac{2x}{3}=\frac{3}{10}-\frac{5}{7}\)

\(\frac{2x}{3}=-\frac{29}{70}\)

\(\Rightarrow2x=-\frac{29}{70}.3=-\frac{87}{70}\)

\(\Rightarrow x=-\frac{87}{70}\div2=-\frac{87}{140}\)

a, \(3,2x+\left(-1,2\right)x+2,7=-4,9\) 9

\(\left(3,2-1,2\right)x+2,7=-4,9\)

\(2x=-7,6\)

\(x=-3,8\)

b, \(\frac{-1}{10}+\frac{2x}{5}+\frac{7}{20}=\frac{1}{10}\)

\(\frac{2x}{5}=\frac{-3}{20}\)

\(40x=-15\)

\(x=\frac{-3}{8}\)

c, \(\frac{5}{7}+\frac{2x}{3}=\frac{3}{10}\)

\(\frac{2x}{3}=\frac{-29}{70}\)

\(140x=-87\)

\(x=\frac{-87}{140}\)

Ta có: \(\frac{x}{2}=\frac{y}{3}\) => \(\frac{x}{8}=\frac{y}{12}\)

\(\frac{y}{4}=\frac{z}{5}\) => \(\frac{y}{12}=\frac{z}{15}\)

=> \(\frac{x}{8}=\frac{y}{12}=\frac{z}{15}\)

Áp dụng t/c của dãy tỉ số bằng nhau, ta có:

\(\frac{x}{8}=\frac{y}{12}=\frac{z}{15}=\frac{x+y-z}{8+12-15}=\frac{10}{5}=2\)

=> \(\hept{\begin{cases}\frac{x}{8}=2\\\frac{y}{12}=2\\\frac{z}{15}=2\end{cases}}\) => \(\hept{\begin{cases}x=16\\y=24\\z=30\end{cases}}\)

\(\frac{x}{2}=\frac{y}{3}\)     \(\left(\text{*}\right)\)

\(\frac{y}{4}=\frac{z}{5}\)       \(\left(\text{*}\text{*}\right)\)

\(x+y-z=10\)     \(\left(\text{*}\text{*}\text{*}\right)\)

\(\left(\text{*}\right)\)\(\Leftrightarrow3x=2y\Leftrightarrow x=\frac{2y}{3}\)

\(\left(\text{*}\text{*}\right)\)\(\Leftrightarrow5y=4z\Leftrightarrow z=\frac{5y}{4}\)  

Cả (*) và (**) thế vào (***)

\(\frac{2y}{3}+y-\frac{5y}{4}=10\Leftrightarrow\frac{5y}{12}=10\Leftrightarrow y=24\)

\(\Leftrightarrow x=16;z=30\)

Vậy ...

                               Bài làm:

Gọi số cây trồng được của lớp 7A, 7B lần lượt là x (cây); y (cây).

Tỉ số giữa số cây trồng được của lớp 7A và lớp 7B là 0,8 nghĩa là x : y =0,8 hay .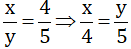

Lớp 7B trồng nhiều hơn lớp 7A là 20 cây nghĩa là y – x = 20.

Theo tính chất dãy tỉ số bằng nhau

Vậy Lớp 7A trồng được 80 cây

Lớp 7B trồng được 100 cây

chúc bn hok tốt 

thuộc j v bn

Gọi số đó là abcd

Theo bài cho : abcd x 4 = dcba

=> abcd = dcba : 4 

Vì dcba là số có 4 chữ số nên dcba < 10> abcd =  dcba : 4 < 10> a  ≤≤ 2

Hơn nữa , a  phải là chữ số chẵn khác 0 nên a  = 2

=>  2bcd x 4 = dcba =>  d > 2 và kết quả d x 4 có chữ số tận cùng bằng 2

=> d = 8

Vậy ta có: 2bc8 x 4 = 8cb2  =>  phép nhân 4 x b không có nhớ  

Mà theo dấu hiệu chia hết cho 4 => b2 chia hết cho 4 => b có thể bằng 1;3;52;72; 92

=> b  chỉ có thể bằng 1

=> 21c8 x 4 = 8c12 => 8000 + 400 + 40c + 32 = 8000 + 100c + 12 

=> 420 = 60c => c = 420 : 60 = 7

Vậy số cần tìm là: 2178

a) Gọi số cần tìm là abcd

Nếu nhân số đó vs 4 thì ta dc số ấy viết theo thứ tự ngược lại là:

abcd.4=dcba

=>dcba chia hết cho 4

Vậy a thuộc 0;2;4;6;8} và a<3

=>a=2

dcba=2bcd.4>2000.4=8000

=> d thuộc {8;9}

Mà 4d<10

->d=8

8cd2=2bc8.4

=>8cb2 chia hết cho 4=>b2 chia hết cho 4

=>b thuộc  {1;3;5;7;9}

Mà 4b<10

=>b=1

8c12=21c8.4

4c+3 có tận cùng là 1

=> 4c là số chẵn và=8

=>c thuộc {2;7}

Vs c=2: 0 thỏa mãn vì 2128.4e8212

Vs c=7 thỏa mãn vì 2178.4=8712

Vậy abcd=2178

\(\text{A = }\frac{\text{-1}}{\text{2011}}-\frac{\text{3}}{\text{11}^2}-\frac{\text{5}}{\text{11}^2.\text{11}}-\frac{\text{7}}{\text{11}^2.\text{11}^2}=\text{ }\frac{\text{-1}}{\text{2011}}-\frac{\text{1}}{\text{11}^2}.\left(3-\frac{\text{5}}{\text{11}}-\frac{\text{7}}{\text{11}^2}\right)\)

\(\text{B = }\text{ }\frac{\text{-1}}{\text{2011}}-\frac{7}{\text{11}^2}-\frac{5}{\text{11}^2.\text{11}}-\frac{3}{\text{11}^2.\text{11}^2}=\frac{\text{-1}}{\text{2011}}-\frac{\text{1}}{\text{11}^2}.\left(7-\frac{5}{\text{11}}-\frac{3}{\text{11}^2}\right)\)

\(\text{Vì }3-\frac{\text{5}}{\text{11}}-\frac{\text{7}}{\text{11}^2}< 7-\frac{5}{\text{11}}-\frac{3}{\text{11}^2}\)

\(\Rightarrow\frac{\text{-1}}{\text{2011}}-\frac{\text{1}}{\text{11}^2}.\left(3-\frac{\text{5}}{\text{11}}-\frac{\text{7}}{\text{11}^2}\right)>\frac{\text{-1}}{\text{2011}}-\frac{\text{1}}{\text{11}^2}.\left(7-\frac{5}{\text{11}}-\frac{3}{\text{11}^2}\right)\)

=> A > B

Vậy A > B

a có: xOy=120 (đề cho) và oAt= 60 (đề cho) ta lại có xOy+tAo=120 + 60 =180 (kề bù) mà 2 góc xOy và tAo ở vị trí trong cùng phía suy ra : oy // At mà AT' là tia đối của tia AT suy ra : tt' // oy

b) ta có xOy = xAt ( 2 góc đồng vị , oy // at ) mà xoy= 120 suy ra xAt=120 vì om là tia phân gica của xOy nên xom = moy = xoy/2 = 60 và on là tia phân giác của xAt xAn=nAt = xAt/2 = 60 mà xOy = xAt ( = 120 ) ta có xAn = xOm (= 60 ) mà 2 góc xAn và xOm ở vị tí đồng vị suy ra : An // Om

các số nhớ thêm độ đấy nhé

k đi

O y x A t m m n K L z

a) góc AOy = 120 ⁰ => góc AOm = 60⁰  

Ta lại có góc  AOt = 60⁰ => At //  Oy ( Cặp góc so le trong )

b) Om ko thể // An

Đánh số các người tham gia từ \(A_1\)đến \(A_{16}\).

Giả sử \(A_1\)thắng nhiều nhất. 

Có: \(\frac{16\times15}{2}=120\)(ván đấu) suy ra \(A_1\)thắng \(\ge\frac{120}{16}=7,5\)

suy ra \(A_1\)thắng ít nhất \(8\)ván. 

Không mất tính tổng quát, giả sử \(A_1\)thắng \(A_2,A_3,...,A_9\).

Giả sử trong những người này \(A_2\)thắng nhiều nhất.

\(A_2,...,A_9\)đánh \(\frac{8\times7}{2}=28\)(ván) suy ra \(A_2\)thắng \(\ge\frac{28}{8}=3,5\)

suy ra \(A_2\)thắng ít nhất \(4\)ván (khi đấu với \(A_3,...,A_9\))

Giả sử \(A_2\)thắng \(A_3,...,A_6\).

Giả sử \(A_3\)thắng nhiều nhất trong những người này. 

\(A_3,...,A_6\)đánh \(\frac{4\times3}{2}=6\)(ván) suy ra \(A_3\)thắng \(\ge\frac{6}{4}=1,5\)

suy ra \(A_3\)thắng ít nhất \(2\)ván. 

Giả sử \(A_3\)thắng \(A_4,A_5\). 

Khi đó giả sử \(A_4\)thắng \(A_5\)thì ta có dãy thỏa mãn là: \(A_1,A_2,A_3,A_4,A_5\). 

Ta có đpcm. 

linh tinh

x=1 nha

x=0 ấn nhầm

cho 1k nhé

Một tam giác vuông có cạnh huyền bằng 26cm và có độ dài các cạnh góc vuông tỉ lệ với 5 và 12. Tính độ dài các cạnh góc vuông?

A. 10 cm, 22 cm

B. 10 cm, 24 cm

C. 12 cm, 24 cm

D. 15 cm, 24 cm

Gọi độ dài 2 cạnh là \(x\), \(y\)( \(x\), \(y\)> 0 )

Theo định lý Pitago ta có : \(\frac{x}{5}=\frac{y}{12}\)\(\Rightarrow\)\(\frac{x^2}{25}=\frac{y^2}{144}=\frac{x^2+y^2}{25+144}\)

= \(\frac{676}{169}=4\)

\(\Leftrightarrow\)\(x^2=25.4\)

\(\Leftrightarrow\)\(x^2=100\)

\(\Leftrightarrow\)\(x=10\)cm

Ta lại có :

\(\Leftrightarrow\)\(y^2=144.4\)

\(\Leftrightarrow\)\(y^2=576\)

\(\Leftrightarrow\)\(y=24\)

Vậy ...................

=> Chọn B

Hok tốt