Tìm x biết: x^2 -9x - 26 = 0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


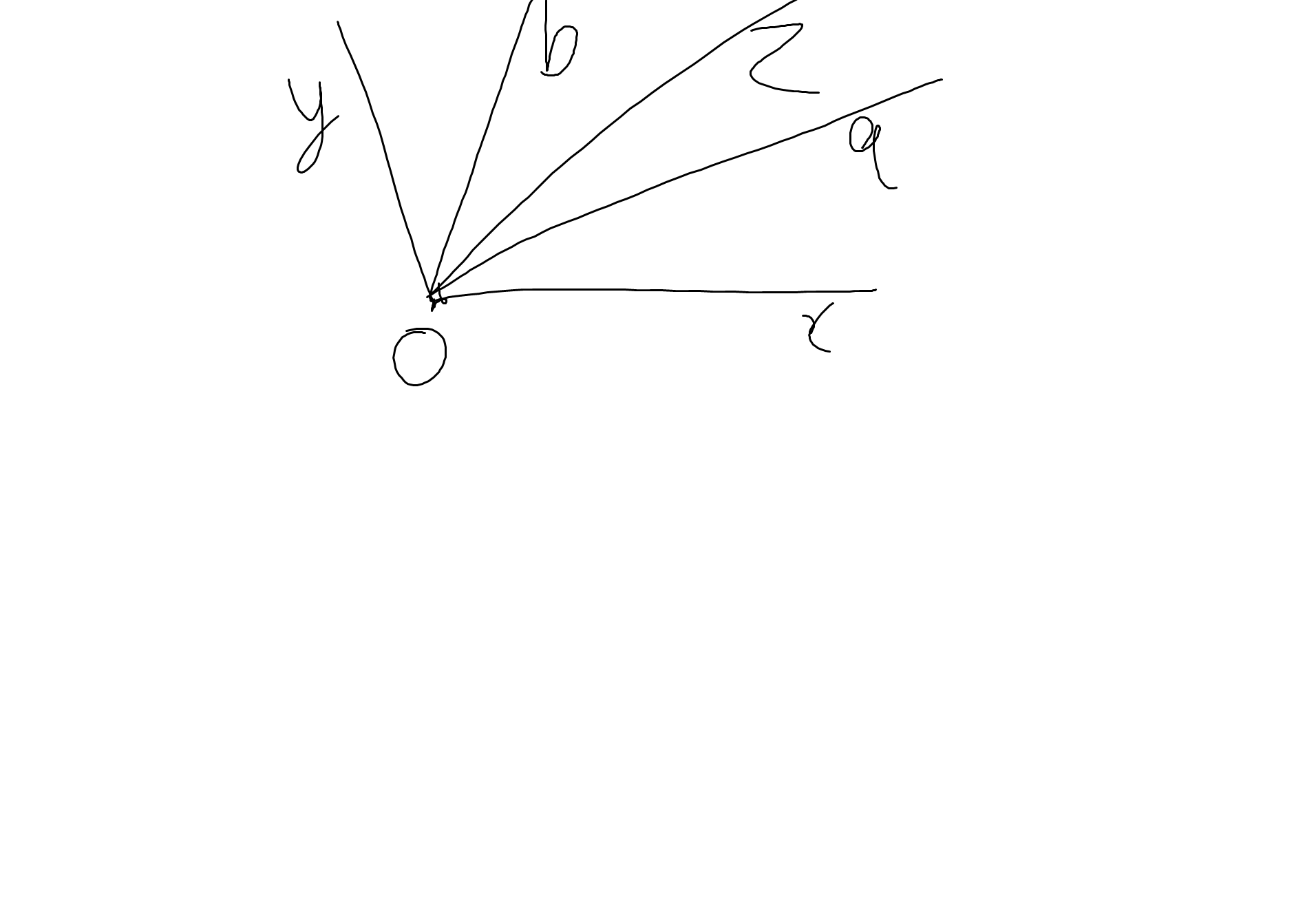
Oa là phân giác của góc xOz
=>\(\widehat{zOa}=\dfrac{\widehat{xOz}}{2}\)
Ob là phân giác của góc zOy
=>\(\widehat{zOb}=\dfrac{\widehat{zOy}}{2}\)
\(\widehat{aOb}=\widehat{zOa}+\widehat{zOb}=\dfrac{1}{2}\left(\widehat{xOz}+\widehat{zOy}\right)\)
\(=\dfrac{1}{2}\cdot\widehat{xOy}=\dfrac{1}{2}\cdot150^0=75^0\)

`(a_1 + a_2+... + a_9)/(a_3+a_6+a_9)`
`= ((a_3+a_6+a_9) + (a_2+a_5+a_8) + (a_1+a_4+a_7))/(a_3+a_6+a_9)`
`<= (3.(a_3+a_6+a_9))/(a_3+a_6+a_9) = 3 < 5`.

a: Sau 3 giờ, xe máy đi được: 3x40=120(km)
Hiệu vận tốc hai xe là 60-40=20(km/h)
Hai xe gặp nhau sau khi ô tô đi được: 120:20=6(giờ)
b: Điểm gặp nhau cách A:
6x60=360(km)

`(7x - 11)^3 = 2^5 . 5^2 + 100`
`=> (7x - 11)^3 = 32 . 25 + 100`
`=> (7x - 11)^3 = 800 + 100`
`=> (7x - 11)^3 = 900`
`=> 7x - 11 =` \(\sqrt[3]{900}\)
`=> 7x = 11 +` \(\sqrt[3]{900}\)
`=> x =` \(\dfrac{11+\sqrt[3]{900}}{7}\)
Vậy ...
Sửa đề:
\(\left(7x-11\right)^2=2^5.5^2+100\)
\(\left(7x-11\right)^2=32.25+100\)
\(\left(7x-11\right)^2=800+100\)
\(\left(7x-11\right)^2=900\)
\(\left(7x-11\right)^2=30^2\)
\(\Rightarrow7x-11=30\)
\(7x=30+11\)
\(7x=41\)
\(x=41\div7\)
\(x=\dfrac{41}{7}\)
Vậy \(x=\dfrac{41}{7}\)

Lớp 2b trồng được số cây là:
1234 + 890 = 2124 (cây)
Trung bình mỗi lớp trồng được là:
(1234 + 2124) : 2 = 1679 (cây)
Đáp số: 1679 cây
*Ở đây dp lớp 2B trồng nhiều hơn lớp 2A là 890 cây nên ta lấy số cây lớp 2A + 890 = số cây lớp 2B.
*Ngoài ra khi tính trung bình cộng, bạn cho số cây mỗi lớp vào phép cộng trong ngoặc rồi mới chia 2 nhé.

a: \(P=4\left(3^2+1\right)\left(3^4+1\right)\left(3^8+1\right)\left(3^{16}+1\right)\left(3^{32}+1\right)\)
\(=\dfrac{\left(3^2-1\right)\left(3^2+1\right)\left(3^4+1\right)\left(3^8+1\right)\left(3^{16}+1\right)\left(3^{32}+1\right)}{2}\)
\(=\dfrac{\left(3^4-1\right)\left(3^4+1\right)\left(3^8+1\right)\left(3^{16}+1\right)\left(3^{32}+1\right)}{2}\)
\(=\dfrac{\left(3^8-1\right)\left(3^8+1\right)\left(3^{16}+1\right)\left(3^{32}+1\right)}{2}\)
\(=\dfrac{\left(3^{16}-1\right)\left(3^{16}+1\right)\left(3^{32}+1\right)}{2}\)
\(=\dfrac{\left(3^{32}-1\right)\left(3^{32}+1\right)}{2}=\dfrac{3^{64}-1}{2}\)
b: \(Q=\left(5^2+1\right)\left(5^4+1\right)\left(5^8+1\right)\left(5^{16}+1\right)\left(5^{32}+1\right)\)
\(=\dfrac{\left(5^2-1\right)\left(5^2+1\right)\left(5^4+1\right)\left(5^8+1\right)\left(5^{16}+1\right)\left(5^{32}+1\right)}{5^2-1}\)
\(=\dfrac{\left(5^4-1\right)\left(5^4+1\right)\left(5^8+1\right)\left(5^{16}+1\right)\left(5^{32}+1\right)}{5^2-1}\)
\(=\dfrac{\left(5^8-1\right)\left(5^8+1\right)\left(5^{16}+1\right)\left(5^{32}+1\right)}{5^2-1}\)
\(=\dfrac{\left(5^{16}-1\right)\left(5^{16}+1\right)\left(5^{32}+1\right)}{5^2-1}\)
\(=\dfrac{\left(5^{32}-1\right)\left(5^{32}+1\right)}{24}=\dfrac{5^{64}-1}{24}\)

a: \(\left|0,5x-2\right|-\left|x+\dfrac{2}{3}\right|=0\)
=>\(\left|\dfrac{1}{2}x-2\right|=\left|x+\dfrac{2}{3}\right|\)
=>\(\left[{}\begin{matrix}\dfrac{1}{2}x-2=x+\dfrac{2}{3}\\\dfrac{1}{2}x-2=-x-\dfrac{2}{3}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}-\dfrac{1}{2}x=2+\dfrac{2}{3}=\dfrac{8}{3}\\\dfrac{3}{2}x=-\dfrac{2}{3}+2=\dfrac{4}{3}\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=\dfrac{8}{3}:\dfrac{-1}{2}=\dfrac{8}{3}\cdot\left(-2\right)=-\dfrac{16}{3}\\x=\dfrac{4}{3}:\dfrac{3}{2}=\dfrac{8}{9}\end{matrix}\right.\)
b:
\(2x-\left|x+1\right|=\dfrac{1}{4}\)
=>\(\left|x+1\right|=2x-\dfrac{1}{4}\)
=>\(\left\{{}\begin{matrix}2x-\dfrac{1}{4}>=0\\\left(2x-\dfrac{1}{4}\right)^2=\left(x+1\right)^2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x>=\dfrac{1}{8}\\\left(2x-\dfrac{1}{4}-x-1\right)\left(2x-\dfrac{1}{4}+x+1\right)=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x>=\dfrac{1}{8}\\\left(x-\dfrac{5}{4}\right)\left(3x+\dfrac{3}{4}\right)=0\end{matrix}\right.\Leftrightarrow x=\dfrac{5}{4}\)
c: \(3x-\left|x+15\right|=\dfrac{5}{4}\)
=>\(\left|x+15\right|=3x-\dfrac{5}{4}\)
=>\(\left\{{}\begin{matrix}3x-\dfrac{5}{4}>=0\\\left(3x-\dfrac{5}{4}\right)^2=\left(x+15\right)^2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x>=\dfrac{5}{12}\\\left(3x-\dfrac{5}{4}-x-15\right)\left(3x-\dfrac{5}{4}+x+15\right)=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x>=\dfrac{5}{12}\\\left(2x-16,25\right)\left(4x+\dfrac{55}{4}\right)=0\end{matrix}\right.\Leftrightarrow x=8,125\)
d: \(\dfrac{3}{2}-\left|\dfrac{5}{4}+3x\right|=\dfrac{1}{4}\)
=>\(\left|3x+\dfrac{5}{4}\right|=\dfrac{3}{2}-\dfrac{1}{4}=\dfrac{5}{4}\)
=>\(\left[{}\begin{matrix}3x+\dfrac{5}{4}=\dfrac{5}{4}\\3x+\dfrac{5}{4}=-\dfrac{5}{4}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}3x=0\\3x=-\dfrac{5}{2}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-\dfrac{5}{6}\end{matrix}\right.\)
e: \(\left|4x-1\right|=\left|3x-\dfrac{1}{2}\right|\)
=>\(\left[{}\begin{matrix}4x-1=3x-\dfrac{1}{2}\\4x-1=-3x+\dfrac{1}{2}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}4x-3x=-\dfrac{1}{2}+1\\4x+3x=\dfrac{1}{2}+1\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=\dfrac{1}{2}\\7x=\dfrac{3}{2}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{2}\\x=\dfrac{3}{14}\end{matrix}\right.\)
f: \(\left|2x-1\right|=\left|x+\dfrac{1}{3}\right|\)
=>\(\left[{}\begin{matrix}2x-1=x+\dfrac{1}{3}\\2x-1=-x-\dfrac{1}{3}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x-x=\dfrac{1}{3}+1\\2x+x=-\dfrac{1}{3}+1\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=\dfrac{4}{3}\\3x=\dfrac{2}{3}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{4}{3}\\x=\dfrac{2}{9}\end{matrix}\right.\)

Xét tổng: S = 1 + 2 + 3 + ... + x
Số lượng số hạng: (x - 1) : 1 + 1 = x (số hạng)
`=>S=((x+1)*x)/2`
\(=>\dfrac{\left(x+1\right)x}{2}=820\\ =>x\left(x+1\right)=1640\\ =>x^2+x-1640=0\\ =>\left(x^2-40x\right)+\left(41x-1640\right)=0\\ =>x\left(x-40\right)+41\left(x-40\right)=0\\ =>\left(x+41\right)\left(x-40\right)=0\\ =>\left[{}\begin{matrix}x=40\\x=-41\end{matrix}\right.\)
Mà x > 0 => x = 40
\(x^2-9x-26=0\)
\(\text{Δ}=\left(-9\right)^2-4\cdot1\cdot\left(-26\right)=81+104=185>0\)
Do đó: Phương trình có hai nghiệm phân biệt là:
\(\left[{}\begin{matrix}x=\dfrac{9-\sqrt{185}}{2}\\x=\dfrac{9+\sqrt{185}}{2}\end{matrix}\right.\)
TY :>