Tổng số viên bi của 2 bạn là:

102 nhân 2=204(viên)

Hải có số viên bi là:

204-97=107(viên)

Đáp số:107 viên bi nhé

số bi của Hải là:
102-97=5

Lời giải:
Quy luật: Mỗi số số hạng, kể từ số hạng thứ ba bằng tổng của số liền trước cộng với số thứ tự rồi trừ đi 1.

Ví dụ: số thứ ba = 5 = 3+3-1

số thứ tư = 8 = 5 + 4- 1

......

Vậy 2 số tiếp theo là:
Số thứ tám = 23+8 - 1= 30 

Số thứ chín = 30 + 9-1=38

Lời giải:

Gọi số thứ nhất là a và số thứ hai là b. Ta có:

$a+b=16,35$ (1) 

$2\times a+3\times b=36,35$ (2) 

Lấy phép tính thứ (2) trừ đi 2 lần phép tính thứ (1):

$2\times a+3\times b-2\times (a+b)=36,35-2\times 16,35$

$2\times a+3\times b-(2\times a+2\times b)=3,65$

$b=3,65$

$a=16,35-b=16,35-3,65=12,7$

Hai lần tổng của số thứ nhất và số thứ hai:

16,35 × 2 = 32,7

Số thứ hai là:

36,35 - 32,7 = 3,65

Số thứ nhất là:

16,35 - 3,65 = 12,7

`#3107.101107`

`a,`

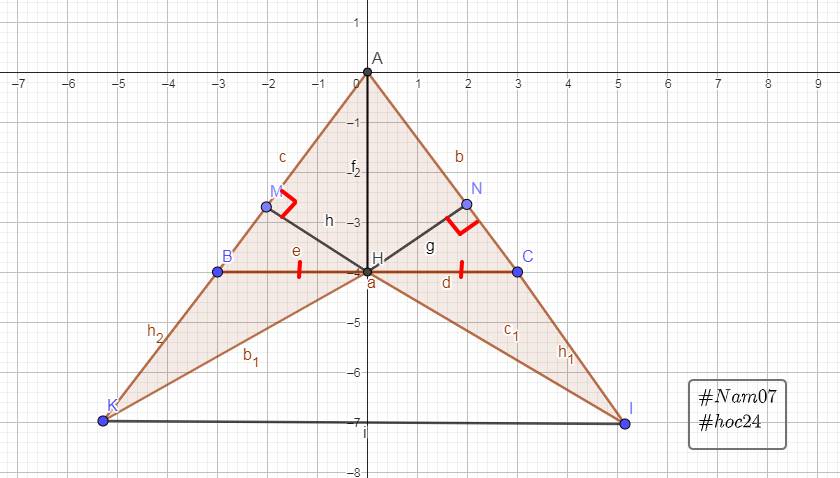
Xét $\triangle ABH$ và $\triangle ACH$:

`AB = AC` $(\triangle ABC$cân tại A`)`

\(\widehat{B}=\widehat{C}\) $(\triangle ABC$cân tại A`)`

`HB = HC ( H` là trung điểm của BC`)`

$=> \triangle ABH = \triangle ACH (c - g - c)$

Vì $\triangle ABH = \triangle ACH$

`=>`\(\widehat{AHB}=\widehat{AHC}\left(\text{2 góc tương ứng}\right)\)

Mà `2` góc này nằm ở vị trí kề bù

`=>` \(\widehat{AHB}+\widehat{AHC}=180^0\)

`=>` \(\widehat{AHB}=\widehat{AHC}=\dfrac{180^0}{2}=90^0\) `=> AH \bot BC`

`b,`

Vì $\triangle ABH = \triangle ACH (a)$

`=>`\(\widehat{BAH}=\widehat{CAH}\left(\text{2 góc tương ứng}\right)\)

Xét $\triangle AHM$ và $\triangle AHN$:

AH chung

\(\widehat{MAH}=\widehat{NAH}\left(CMT\right)\)

\(\widehat{AMH}=\widehat{ANH}\left(=90^0\right)\)

$=> \triangle AHM = \triangle AHN (ch - gn)$

`c,`

Xét $\triangle HMB$ và $\triangle HNC$:

\(\widehat{HMB}=\widehat{HNC}\left(=90^0\right)\)

`HB = HC` `(`gt`)`

\(\widehat{HBM}=\widehat{HCN}\) $(\triangle ABC$ cân tại A`)`

$=> \triangle HMB = \triangle HNC (ch - gn)$

`=>`\(\widehat{BHM}=\widehat{CHN}\left(2\text{ góc tương ứng}\right)\) `(1)`

Vì \(\left\{{}\begin{matrix}\widehat{MHB}+\widehat{KHB}=\widehat{MHK}\\\widehat{NHC}+\widehat{IHC}=\widehat{NHI}\end{matrix}\right.\)

Mà \(\widehat{MHK}=\widehat{NHI}\left(\text{đối đỉnh}\right)\) `(2)`

Từ `(1)` và `(2)` `=>` \(\widehat{KHB}=\widehat{IHC}\)

Xét $\triangle KHB$ và $\triangle IHC$:

\(\widehat{KBH}=\widehat{ICH}\left(\widehat{ABC}=\widehat{ACB}\right)\)

`HB = HC`

\(\widehat{KHB}=\widehat{IHC}\)

$=> \triangle KHB = \triangle IHC (g - c - g)$

`=> BK = CI` `(2` cạnh tương ứng`)`

Ta có:

`AK = AB + BK`

`AI = AC + CI`

Mà `AB = AC; BK = CI`

$=> AK = AI => \triangle AIK$ cân tại A.

Lời giải:

Tổng của số trừ và hiệu chính là số bị trừ.

Mà tổng của số trừ, hiệu và số bị trừ là 64 nên tổng của số trừ và hiệu là: $64:2=32$ 

Hiệu của hiệu và số trừ: $2$ 

Hiệu là: $(32+2):2=17$

Số trừ là: $17-2=15$ 

Số bị trừ là: $17+15=32$

a) 16,27+10:8

 = 16,27+1,25

 = 17,52

b) 45-135:72

 = 45-1,875

 = 43,125

Lời giải:
$A=[(-1)+5]+[(-9)+13]+....+[(-41)+45]$

$=4+4+4+....+4$
Số lần xuất hiện của 4 là: $[(45-1):4+1]:2=6$

$A=4\times 6=24$

-------------------------

$B=(1-2-3+4)+(5-6-7+8)+....+(997-998-999+1000)$
$=0+0+.....+0=0$