Lời giải:

a.

$8750:35=250$

$23520:56=420$

$11780:42=280$ dư 20$

b.

$2996:28=107$

$2420:12=201$ dư $8$

$13870:45=308$ dư $10$

Tổng số học sinh lớp 6:

25 + 50 + 70 + 45 + 60 = 250 (học sinh)

Chọn C

.

A) 8750 : 35 = 250

23520 : 56 = 420

11780 : 42 = 5890/21

B) 2996 : 28 = 107

2420 : 12 = 605/3

13870 : 45 = 2774/9

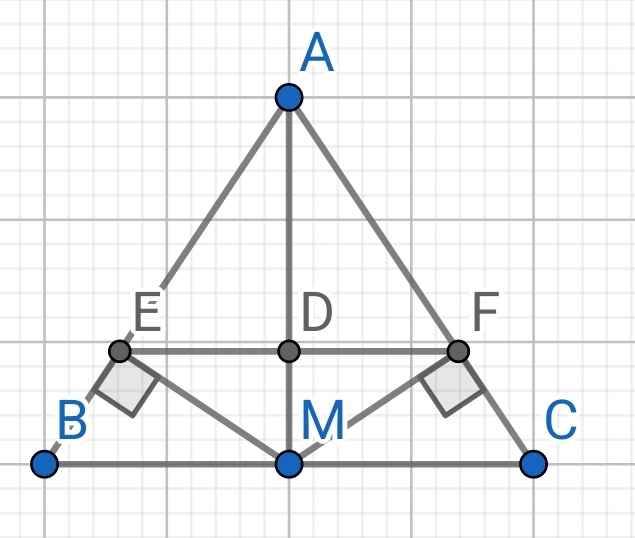 a) Do M là trung điểm của BC (gt)

⇒ BM = CM

Do ∆ABC cân tại A (gt)

⇒ AB = AC

Xét ∆AMB và ∆AMC có:

AM là cạnh chung

AB = AC (cmt)

BM = CM (cmt)

⇒ ∆AMB = ∆AMC (c-c-c)

b) Sửa đề:

Chứng minh AM EF

Giải:

Gọi D là giao điểm của AM và EF

Do ∆AMB = ∆AMC (cmt)

⇒ ∠MAB = ∠MAC (hai góc tương ứng)

⇒ ∠MAE = ∠MAF

Xét hai tam giác vuông: ∆MAE và ∆MAF có:

AM là cạnh chung

∠MAE = ∠MAF (cmt)

⇒ ∆MAE = ∆MAF (cạnh huyền - góc nhọn)

⇒ AE = AF (hai cạnh tương ứng)

Do ∠MAE = ∠MAF (cmt)

⇒ ∠DAE = ∠DAF 

Xét ∆ADE và ∆ADF có:

AD là cạnh chung

∠DAE = ∠DAF (cmt)

AE = AF (cmt)

⇒ ∆ADE = ∆ADF (c-g-c)

⇒ ∠ADE = ∠ADF (hai góc tương ứng)

Mà ∠ADE + ∠ADF = 180⁰ (kề bù)

⇒ ∠ADE = ∠ADF = 180⁰ : 2 = 90⁰

⇒ AD ⊥ EF

.

A B C H D E M

a/

Xét tg MAB và tg MEC có

MB=MC (gt); MA=ME (gt)

\(\widehat{AMB}=\widehat{EMC}\) (góc đối đỉnh)

=> tg MAB = tg MEC (c.g.c)

b/

Ta có  tg MAB = tg MEC (cmt) \(\Rightarrow\widehat{BAM}=\widehat{CEM}\) 

Hai góc trên ở vị trí so le trong => AB//CE

c/

Xét tg vuông ABH và tg vuông DBH có

HA=HD (gt); BH chung => tg ABH = tg DBH (hai tg vuông có 2 cạnh góc vuông bằng nhau) => AB=BD(1)

Ta có tg MAB = tg MEC (cmt) => AB=CE (2)

Từ (1) và (2) => BD=CE

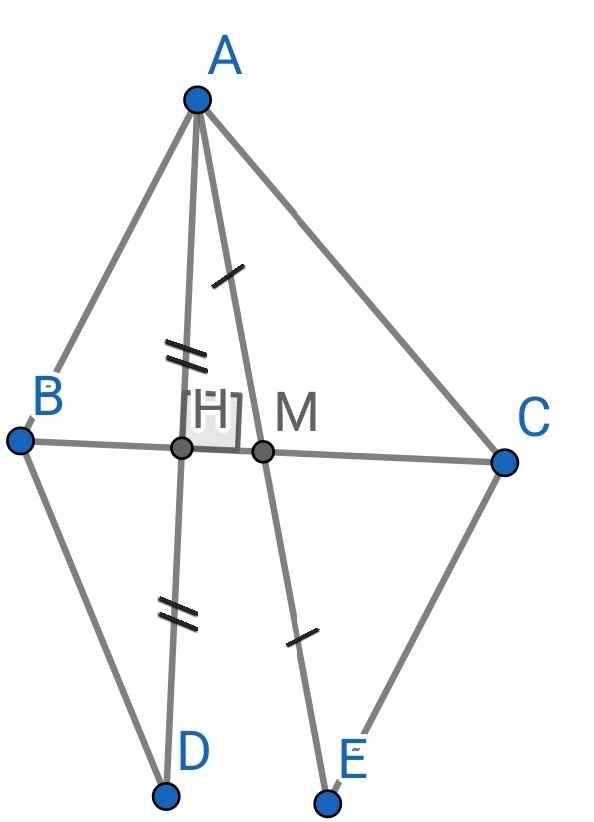 a) Do M là trung điểm của BC (gt)

⇒ BM = MC

Xét ∆MAB và ∆MEC có:

BM = MC (cmt)

∠AMB = ∠EMC (đối đỉnh)

AM = ME (gt)

⇒ ∆MAB = ∆MEC (c-g-c)

b) Do ∆MAB = ∆MEC (cmt)

⇒ ∠MAB = ∠MEC (hai góc tương ứng)

Mà ∠MAB và ∠MEC là hai góc so le trong)

AB // CE

c) Xét hai tam giác vuông: ∆AHB và ∆DHB có:

BH là cạnh chung

AH = HD (gt)

⇒ ∆AHB = ∆DHB (hai cạnh góc vuông)

⇒ AB = BD (hai cạnh tương ứng)

Do ∆MAB = ∆MEC (cmt)

⇒ AB = CE (hai cạnh tương ứng)

Mà AB = BD (cmt)

⇒ BD = CE

.

.

Sửa đề:

Tìm ba số a, b, c biết:

5a = 8b, b = 3c và a - 2b + c = 34

Giải:

5a = 8b ⇒ a/8 = b/5 ⇒ a/24 = b/15 (1)

b = 3c ⇒ b/3 = c/1 ⇒ b/15 = c/5 (2)

Từ (1) và (2) ⇒ a/24 = b/15 = c/5

⇒ a/24 = 2b/30 = c/5

Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:

a/24 = 2b/30 = c/5 = (a - 2b + c)/(24 - 30 + 5) = 34/(-1) = -34

a/24 = -34 ⇒ a = -34.24 = -816

b/15 = -34 ⇒b = -34.15 = -510

c/5 = -34 ⇒ c = -34.5 = -170

Vậy a = -816; b = -510; c = -170

.

giúp tui

.

Lời giải:

Gọi chiều rộng HCN là $a$ thì chiều dài HCN là $\frac{4}{3}\times a$ (cm) 

Ta có:

$\frac{4}{3}\times a\times a=48$

$a\times a=48: \frac{4}{3}$

$a\times a=36=6\times 6$

Suy ra $a=6$ (cm) 

Vậy chiều rộng hcn là $6$ cm. Chiều dài hcn là: $6\times \frac{4}{3}=8$ (cm) 

Chu vi hcn: $2\times (6+8)=28$ (cm)

0,5 nhé