Tìm a để đa thức (x^2 + 6x + a) chia hết cho (x - 2)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bạn xem lại đề xem chứ mình thay \(n=3,4,5,6\) đều không thỏa.

Bài 1 : (4a - b).(4a + b) = 16a2 + (-b2)
(\(x^2y\) + 2y)(\(x^2\)y - 2y = \(x^4\).y2 + (- 4y2)
(\(\dfrac{3}{4}\)\(x\) + \(\dfrac{3}{5}\)y)(\(\dfrac{3}{5}\)y - \(\dfrac{3}{4}\)\(x\)) = \(\dfrac{9}{25}\)y2 + (- \(\dfrac{9}{16}\)\(x^2\))
2; (\(x+2\))(\(x^2\) - 2\(x\) + 4) = \(x^3\) + 8
(3\(x\) + 2y)(9\(x^2\) - 6\(xy\) + 4y2) = 27\(x^3\) + 8y3
3, (5- 3\(x\))(25 + 15\(x\) + 9\(x^2\)) = 125 + ( -27\(x^3\))
(\(\dfrac{1}{2}\)\(x\) - \(\dfrac{1}{5}\)y).(\(\dfrac{1}{4}\)\(x^2\) + \(\dfrac{1}{10}\)\(xy\) + \(\dfrac{1}{25}\)y2 = \(\dfrac{1}{8}\)\(x^3\) + (-\(\dfrac{1}{125}\)y3)

Lời giải:
1. $9x^2+12x+4=(3x)^2+2.3x.2+2^2=(3x+2)^2$
2. $4y^2-20y+25=(2y)^2-2.2y.5+5^2=(2y-5)^2$
3. $27x^3+54x^2y+36xy^2+8y^3=(3x)^3+3.(3x)^2.2y+3.3x.(2y)^2+(2y)^3$
$=(3x+2y)^3$
4. $\frac{1}{8}x^3-\frac{3}{2}x^2+\frac{3}{2}x-1=(\frac{1}{2}x)^3-3.(\frac{1}{2}x)^2.1+3.\frac{1}{2}x.1-1^3=(\frac{1}{2}x-1)^3$

Từ đề bài ta có :
\(a+b+c=0< =>\left(a+b+c\right)^2=0< =>a^2+b^2+c^2+2ab+2ac+2bc=0\)
Mà \(a^2+b^2+c^2=1\) < = > 1 + 2 ( ab + ac + bc ) = 0
< = > 2 ( ab + ac + bc ) = -1
< = > ab + ac + bc = -1/2
\(< =>\left(ab+ac+bc\right)^2=\left(-\dfrac{1}{2}\right)^2< =>\left(ab\right)^2+\left(ac\right)^2+\left(bc\right)^2+2a^2bc+2ab^2c+2abc^2=\dfrac{1}{4}\)
\(< =>\left(ab\right)^2+\left(ac\right)^2+\left(bc\right)^2+2abc\left(a+b+c\right)=\dfrac{1}{4}\)
\(< =>\left(ab\right)^2+\left(ac\right)^2+\left(bc\right)^2=\dfrac{1}{4}\)
Lại có từ \(a^2+b^2+c^2=1\)
\(< =>\left(a^2+b^2+c^2\right)^2=1< =>a^4+b^4+c^4+2\left[\left(ab\right)^2+\left(ac\right)^2+\left(bc\right)^2\right]=1\)
\(< =>a^4+b^4+c^4+2.\dfrac{1}{4}=1< =>a^4+b^4+c^4+\dfrac{1}{2}=1< =>a^4+b^4+c^4=1-\dfrac{1}{2}=\dfrac{1}{2}\left(đpcm\right)\)

a) Ta có góc B = 105 độ và góc D = 75 độ.
Vì AB = BC = CD, suy ra tam giác ABC và tam giác BCD là tam giác cân.
Do đó, ta có góc ABC = góc BAC và góc BCD = góc BDC.
Vì góc BAC + góc ABC + góc BCA = 180 độ (tổng các góc trong tam giác ABC bằng 180 độ),
thay giá trị vào ta có góc BAC + góc BAC + góc BCA = 180 độ.
Suy ra góc BAC + góc BCA = 180 độ - góc BAC = góc ABC.
Tương tự, ta có góc BCD + góc BDC = 180 độ - góc BDC = góc BCD.
Vậy ta có góc BAC = góc ABC = góc BCA và góc BCD = góc BDC = góc BCD.
Do đó, AC là tia phân giác của góc A.
b) Ta đã chứng minh được AC là tia phân giác của góc A.
Vì AB = BC = CD, suy ra tam giác ABC và tam giác BCD là tam giác cân.
Vì góc BAC = góc ABC và góc BCD = góc BDC,
nên ta có góc BAC = góc ABC = góc BCA và góc BCD = góc BDC = góc BCD.
Vậy ta có AB || CD.
Do đó, ABCD là hình thang cân.

`M=2(x^3 -y^3 )-3(x^2 +y^2)`
`M=2(x-y)(x^2 +xy+y^2 )-3x^2 -3y^2`
`M=2x^2 +2xy+2y^2 -3x^2 -3y^2`
`M=-x^2 +2xy-y^2`
`M=-(x^2 -2xy+y^2)`
`M=-(x-y)^2`
`M=-(1)^2`
`M=-1`
\(M=2\left(x^3-y^3\right)-3\left(x^2-y^2\right)\)
\(M=2\left(x-y\right)\left(x^2+xy+y^2\right)-3\left(x-y\right)\left(x+y\right)\)
\(M=2\left[x^2+x\left(x-1\right)+\left(x-1\right)^2\right]-3\left(2x-1\right)\)
\(M=2\left(x^2+x^2-x+x^2-2x+1\right)-6x+3\)
\(M=6x^2-12x+5\)
Đề bài yêu cầu tính giá trị nhưng mình cũng không rõ là giá trị gì nên mình làm đến đây thôi nhé.

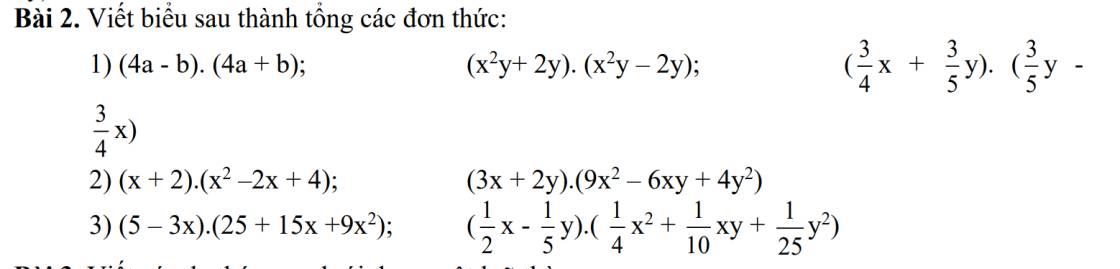 mong
mong 

Để đa thức \(P\left(x\right)=x^2+6x+a\) chia hết cho \(\left(x-2\right)\) thì \(x^2+6x+a\) phải có nghiệm là \(2\)
Điều này có nghĩa là \(P\left(2\right)=0\Leftrightarrow2^2+6.2+a=0\Leftrightarrow a=-16\)