Một hình chữ nhật có chu vi gấp 3 lần chiều dài. Vậy chiều dài của hình chữ nhật đó gấp mấy lần chiều rộng?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Em cần làm gì với dãy số này thì nói rõ ràng và cụ thể ra em nhé!

`2/5 + 3/4 + 1/4`
`= 2/5 + (3/4 + 1/4) `
`= 2/5 + 4/4`
`= 2/5 + 1`
`= 2/5 + 5/5`
`= 7/5`

\(\dfrac{2}{3}\) + \(\dfrac{4}{5}\) = \(\dfrac{10}{15}\) + \(\dfrac{12}{15}\) = \(\dfrac{22}{25}\)
\(\dfrac{2}{3}+\dfrac{4}{5}=\dfrac{10}{15}+\dfrac{12}{15}=\dfrac{10+12}{15}=\dfrac{22}{15}\)

\(\left(x^2+3x\right)^2-2\left(x^2+3x\right)-8\)
\(=\left(x^2+3x\right)^2-4\left(x^2+3x\right)+2\left(x^2+3x\right)-8\)
\(=\left(x^2+3x-4\right)\left(x^2+3x+2\right)\)
\(=\left(x+4\right)\left(x-1\right)\cdot\left(x+2\right)\left(x+1\right)\)


\(\dfrac{x}{y}\) = 5,4 và \(\dfrac{x}{y^2}\) = 6 (y ≠ 0)
(\(\dfrac{x}{y}\)) = 5,42 ⇒ \(\left(\dfrac{x}{y}\right)^2\)= 29,16;
Thay \(\dfrac{x}{y^2}\) = 6 vào biểu thức (\(\dfrac{x}{y}\))2 = 29,16 ta được:
\(x.\)6 = 29,16 ⇒ \(x=\) 29,16 : 6 ⇒ \(x\) = 4,86
Thay \(x=4,86\) vào biểu thức \(\dfrac{x}{y}\) = 5,4 ta được
\(4,86\) : y = 5,4 ⇒ y = 4,86 : 5,4 ⇒ y = 0,9
Vậy (\(x;y\)) = (4,86; 0,9)

`(x-3)(x+4) > 0`
`=> x - 3` và `x + 4` cùng dấu
Trường hợp 1: `{(x-3>0),(x+4>0):}`
`=> {(x>3),(x>-4):}`
`=> x > 3`
Trường hợp 2: `{(x-3<0),(x+4<0):}`
`=> {(x<3),(x<-4):}`
`=> x < -4`
Vậy ...
a; (\(x-3\))(\(x+4\)) > 0
\(x-3=0\) ⇒ \(x=3\)
\(x+4\) = 0 ⇒ \(x=-4\)
Lập bảng ta có:
| \(x\) | - 4 3 |
| \(x-3\) | - - 0 + |
| \(x+4\) | - 0 + + |
| (\(x-3\))(\(x+4\)) | + 0 - 0 + |
Theo bảng trên ta có:
\(x\) \(\in\) (- ∞; -4) \(\cup\)(3 ; + ∞)

30.(\(x-\dfrac{7}{12}\)) - 24\(x\) = 100 + 6.(\(x\) - \(\dfrac{3}{4}\))
30\(x\) - \(\dfrac{35}{2}\) - 24\(x\) = 100 + 6\(x\) - \(\dfrac{9}{2}\)
30\(x\) - 24\(x\) - 6\(x\) = 100 - \(\dfrac{9}{2}\) + \(\dfrac{35}{2}\)
6\(x\) - 6\(x\) = 100 - (\(\dfrac{9}{2}\) - \(\dfrac{35}{2}\))
0 = 100 + 13
0 = 113 (vô lý)
Vậy không có giá trị nào của \(x\) thỏa mãn đề bài.
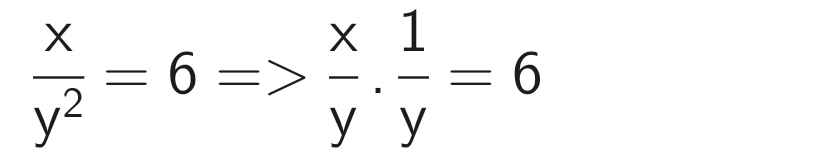
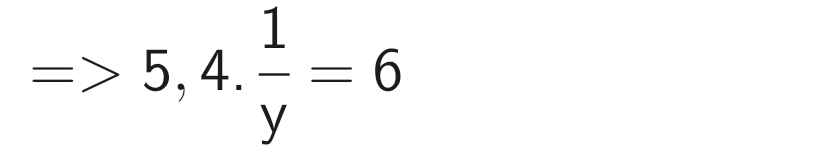
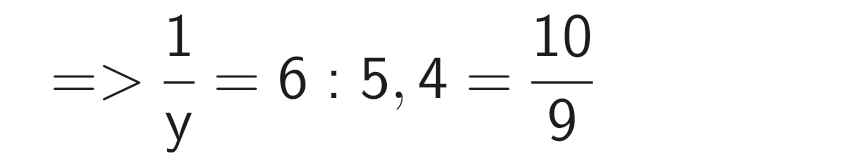
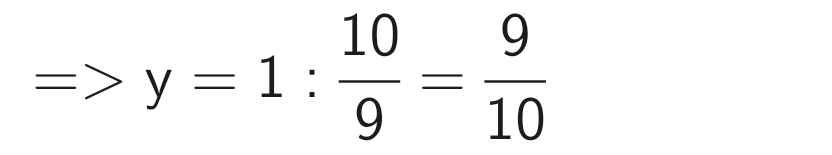

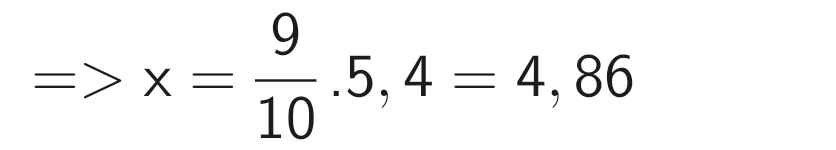
Chu vi gấp 3 lần chiều dài
=>2(Chiều dài+Chiều rộng)=3 chiều dài
=>2 chiều dài+2 chiều rộng=3chiều dài
=>Chiều rộng=-chiều dài
=>Đề sai rồi bạn