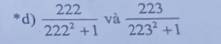
So sánh số hữu tỉ ạ em cảm ơn
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Ta sắp xếp các chữ số còn lại (0, 2, 3, 4, 5, 6, 7, 9) từ nhỏ đến lớn và chọn những số nhỏ nhất:
- Hàng chục nghìn: 1 (nhỏ nhất nhưng không thể vì đã dùng ở hàng đơn vị)
- Hàng chục nghìn: 2 (số nhỏ nhất chưa dùng)
- Hàng trăm: 0 (số nhỏ nhất chưa dùng)
- Hàng chục: 3 (số nhỏ nhất chưa dùng)
Ta có:
- Chữ số hàng chục nghìn: 2
- Chữ số hàng nghìn: 8
- Chữ số hàng trăm: 0
- Chữ số hàng chục: 3
- Chữ số hàng đơn vị: 1
Số nhỏ nhất là 28031
+ Số có 5 chữ số có dạng: \(\overline{abcde}\); Theo bài ra ta có: b = 8; e = 1
+ Các chữ số còn lại là: 0; 2; 3; 4; 5; 6; 7; 9
+ Để được số bé nhất có 5 chữ số khác nhau thì các chữ số ở hàng cao phải bé nhất có thể và các chữ số phải khác nhau mà 0 không thể đứng đầu nên:
a = 2; c = 0; d = 3 Thay a= 2; b = 8; c = 0; d = 3; e = 1 vào biểu thức
\(\overline{abcde}\) ta được số: 28031
+ Vậy số thoả mãn đề bài là: 28031
Đáp số: 28031

Số có 5 chữ số khác nhau thì chữ số hàng nghìn và hàng đơn vị cũng phải khác nhau, chữ số hàng nghìn là 8 hàng đơn vị cũng là 8 không thoả mãn đề bai nên không tồn tại số nào như yêu cầu

Bài 3
a; m - 2021 = 0 ⇒ m = 2021
Lập bảng ta có:
| m | 2021 |
| m - 2021 | - 0 + |
| 2024 | + + |
| \(x=\dfrac{m-2021}{2024}\) | - 0 + |
Theo bảng trên ta có \(x\) là số hữu tỉ dương khi và chỉ khi m > 2021
Vậy m > 2021
Bài 3b;
Bài 3
a; m - 2021 = 0 ⇒ m = 2021
Lập bảng ta có:
| m | 2021 |
| m - 2021 | - 0 + |
| 2024 | + + |
| \(x=\dfrac{m-2021}{2024}\) | - 0 + |
Theo bảng trên ta có \(x\) là số hữu tỉ âm khi và chỉ khi m < 2021
Vậy m < 2021

Ta có: \(4=\dfrac{20}{5}\)
Mà: \(20< 21\)
\(\Rightarrow\dfrac{20}{5}< \dfrac{21}{5}\)
\(\Rightarrow4< \dfrac{21}{5}\)

Mình thấy dãy số này ko tuân theo 1 quy tắc số hc nào hết

Đặt 222=a
=>\(\dfrac{222}{222^2+1}=\dfrac{a}{a^2+1};\dfrac{223}{223^2+1}=\dfrac{\left(a+1\right)^2}{\left(a+1\right)^2+1}\)
\(\dfrac{a^2}{a^2+1}-\dfrac{\left(a+1\right)^2}{\left(a+1\right)^2+1}\)
\(=\dfrac{a^2\left[\left(a+1\right)^2+1\right]-\left(a+1\right)^2\left(a^2+1\right)}{\left(a^2+1\right)\left[\left(a+1\right)^2+1\right]}\)
\(=\dfrac{a^2\left(a^2+2a+2\right)-\left(a^2+2a+1\right)\left(a^2+1\right)}{\left(a^2+1\right)\left[\left(a+1\right)^2+1\right]}\)
\(=\dfrac{a^4+2a^3+2a^2-a^4-a^2-2a^3-2a-a^2-1}{\left(a^2+1\right)\left[\left(a+1\right)^2+1\right]}\)
\(=\dfrac{-2a-1}{\left(a^2+1\right)\left[\left(a+1\right)^2+1\right]}< 0\)
=>\(\dfrac{222}{222^2+1}< \dfrac{223}{223^2+1}\)