x + (1/2 - x )1/3 = 7/6-x
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Để rút gọn biểu thức, ta sẽ thực hiện các phép tính và kết hợp các thành phần tương tự: P(2x-1).4x^2 + 2x + 1 + (x+1)x^2 - x + 1 = P(8x^3 - 4x^2) + 2x + 1 + x^3 + x^2 - x + 1 = P(8x^3) - P(4x^2) + x^3 + (2x-x) +(1+1) = **8Px^3 - 4Px^2**+ x^3 **+ x**+ **2** Vậy biểu thức đã được rút gọn thành: **8Px³ - 4Px²+x³+x+2**

a) \(\left(x-5\right)^2=\left(3+2x\right)^2\)
\(\Rightarrow\left(3+2x\right)^2-\left(x-5\right)^2=0\)
\(\Rightarrow\left(3+2x+x-5\right)\left(3+2x-x+5\right)=0\)
\(\Rightarrow\left(3x-2\right)\left(x+8\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}3x-2=0\\x+8=0\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=\dfrac{2}{3}\\x=-8\end{matrix}\right.\)
b) \(27x^3-54x^2+36x=9\)
\(\Rightarrow27x^3-54x^2+36x-9=0\)
\(\Rightarrow27x^3-54x^2+36x-8+8-9=0\)
\(\Rightarrow\left(3x-2\right)^3-1=0\)
\(\Rightarrow\left(3x-2-1\right)\left[\left(3x-2\right)^2+3x-2+1\right]=0\)
\(\Rightarrow\left(3x-3\right)\left[\left(3x-2\right)^2+3x-2+\dfrac{1}{4}-\dfrac{1}{4}+1\right]=0\)
\(\Rightarrow\left(3x-3\right)\left[\left(3x-2+\dfrac{1}{2}\right)^2+\dfrac{3}{4}\right]=0\)
\(\Rightarrow\left(3x-3\right)\left[\left(3x-\dfrac{3}{2}\right)^2+\dfrac{3}{4}\right]=0\left(1\right)\)
mà \(\left(3x-\dfrac{3}{2}\right)^2+\dfrac{3}{4}>0,\forall x\)
\(\left(1\right)\Rightarrow3x-3=0\Rightarrow3x=3\Rightarrow x=1\)
(\(x-5\))2 = (3 +2\(x\))2 ⇒ \(\left[{}\begin{matrix}x-5=3+2x\\x-5=-3-2x\end{matrix}\right.\) ⇒ \(\left[{}\begin{matrix}x=-8\\x=\dfrac{2}{3}\end{matrix}\right.\) vậy \(x\in\){-8; \(\dfrac{2}{3}\)}
27\(x^3\) - 54\(x^2\) + 36\(x\) = 9
27\(x^3\) - 54\(x^2\) + 36\(x\) - 8 = 1
(3\(x\) - 2)3 = 1 ⇒ 3\(x\) - 2 = 1 ⇒ \(x\) = 1


\(4x^2+4x+1=\left(x-2\right)^2\\ \Leftrightarrow\left(2x+1\right)^2=\left(x-2\right)^2\\ \Leftrightarrow\left[{}\begin{matrix}2x+1=x-2\\2x+1=2-x\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=-3\\x=\dfrac{1}{3}\end{matrix}\right.\)

\(1,\left(x-3\right)^2+3-x=0\)
\(\Leftrightarrow x^2-6x+9+3-x=0\)
\(\Leftrightarrow x^2-7x+12=0\)
\(\Leftrightarrow x^2-3x-4x+12=0\)
\(\Leftrightarrow\left(x-3\right)\left(x-4\right)=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-3=0\\x-4=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=3\\x=4\end{matrix}\right.\)
Vậy.........
\(\left(x-3\right)^2+3-x=0\\ \Leftrightarrow x^2-6x+9+3-x=0\\ \Leftrightarrow x^2-7x+12=0\\ \Leftrightarrow x^2-3x-4x+12=0\\ \Leftrightarrow x\left(x-3\right)-4\left(x-3\right)=0\\ \Leftrightarrow\left(x-3\right)\left(x-4\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x-3=0\\x-4=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=3\\x=4\end{matrix}\right.\)
Vậy \(S=\left\{3;4\right\}\)

\(\left\{{}\begin{matrix}3x-6y+2z=-4\\3x-y-3z=1\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}3x-6y+2z=-4\\3x-y-3z=1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}3x-6y=-4-2z\\3x-y=1+3z\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}5y=1+3z+4+2z\\3x-y=1+3z\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}5y=5+5z\\3x=y+1+3z\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}y=1+z\\3x=1+z+1+3z\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}y=1+z\\x=\dfrac{4z+6}{3}\end{matrix}\right.\)
\(S=9x^2-8\left(y^2+z^2\right)\)
\(S=9\left(\dfrac{4z+2}{3}\right)^2-8\left[\left(1+z\right)^2+z^2\right]\)
\(S=9.\dfrac{16z^2+16z+4}{9}-8\left[1+2z+z^2+z^2\right]\)
\(S=16z^2+16z+4-8-16z-16z^2\)
\(S=-4\)
Đính chính \(x=\dfrac{4z+2}{3}\) không phải \(x=\dfrac{4z+6}{3}\)

Bài 9A:
\(a,\left(x+5\right)^2-\left(x-5\right)^2-2x+1=0\\ \Leftrightarrow\left(x^2+10x+25\right)-\left(x^2-10x+25\right)-2x+1=0\\ \Leftrightarrow x^2-x^2+10x+10x-2x=-1-25+25\\ \Leftrightarrow18x=-1\\ \Leftrightarrow x=-\dfrac{1}{18}\\ b,\left(2x-7\right)^2-\left(x+3\right)^2=3x^2+6\\ \Leftrightarrow4x^2-28x+49-x^2-6x-9-3x^2-6=0\\ \Leftrightarrow4x^2-x^2-3x^2-28x-6x=6+9-49\\ \Leftrightarrow22x=-34\\ \Leftrightarrow x=-\dfrac{17}{11}\\ c,\left(3x+2\right)^2-9\left(x-5\right)\left(x+5\right)=225-5x\\ \Leftrightarrow9x^2+12x+4-9\left(x^2-25\right)=225-5x\\ \Leftrightarrow9x^2-9x^2+12x+5x=225-4+9.25\\ \Leftrightarrow17x=446\\ \Leftrightarrow x=\dfrac{446}{17}\)
Sao bài này câu nào x cũng k nguyên ta, hơi xấu hi
9B
\(a,\left(4x-1\right)^2-4\left(2x-3\right)^2-x-4=0\\ \Leftrightarrow16x^2-8x+1-4\left(4x^2-12x+9\right)-x-4=0\\ \Leftrightarrow16x^2-16x^2-8x+48x-x=4+36-1\\ \Leftrightarrow39x=39\\ \Leftrightarrow x=1\\ b,x\left(x-5\right)-\left(4-x\right)^2=7x+1\\ \Leftrightarrow x^2-5x-\left(16-8x+x^2\right)-7x-1=0\\ \Leftrightarrow x^2-x^2-5x+8x-7x=1+16\\ \Leftrightarrow-4x=17\\ \Leftrightarrow x=\dfrac{-17}{4}\\ c,\left(2x-6\right)\left(x+3\right)=2\left(x-3\right)^2\\ \Leftrightarrow2x^2-6x+6x-18=2\left(x^2-6x+9\right)\\ \Leftrightarrow2x^2-2x^2-6x+6x+12x=18+18\\ \Leftrightarrow12x=36\\ \Leftrightarrow x=\dfrac{36}{12}=3\)

(\(x+1\))2 - (\(x+1\)) = 0
(\(x+1\))(\(x+1-1\)) =0
(\(x+1\))\(x\) = 0
\(\left[{}\begin{matrix}x+1=0\\x=0\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=-1\\x=0\end{matrix}\right.\)
Vậy \(x\in\){ -1; 0}
Giải bằng cách phân tích đa thức thành nhân tử nhé mn
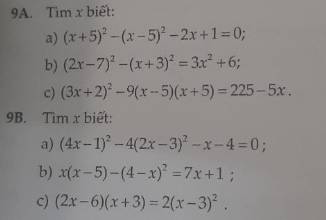
\(x+\left(\dfrac{1}{2}-x\right).\dfrac{1}{3}=\dfrac{7}{6}-x\)
\(\Leftrightarrow x+\dfrac{1}{6}-\dfrac{1}{3}x=\dfrac{7}{6}-x\)
\(\Leftrightarrow2x-\dfrac{1}{3}x=1\)
\(\Leftrightarrow6x-x=3\Leftrightarrow5x=3\Rightarrow x=\dfrac{3}{5}\)
x+(\(\dfrac{1}{2}\)-x)\(\dfrac{1}{3}\)=\(\dfrac{7}{6}\)-x
=>\(\dfrac{1}{6}\)-\(\dfrac{1}{3}\)x=\(\dfrac{7}{6}\)-x-x=\(\dfrac{7}{6}\)-2x
=>\(\dfrac{1}{6}\)-\(\dfrac{7}{6}\)=-2x+\(\dfrac{1}{3}\)x
=>-1=\(\dfrac{-5}{3}\)x
=>1=\(\dfrac{5}{3}\)x
=>x=1:\(\dfrac{5}{3}\)=\(\dfrac{3}{5}\).