
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Vì x và y tỉ lệ thuận nên
\(\dfrac{x}{y}=\dfrac{x'}{y'}\\ \Rightarrow\dfrac{5}{8}=\dfrac{8}{y'}\\ \Rightarrow y'=19,2\)
Lời giải:
Gọi $k$ là hệ số tỉ lệ của $y$ với $x$. Khi đó: $y=kx$
Thay $x=5; y=8$ thì: $8=k.5\Rightarrow k=\frac{8}{5}$
$\Rightarrow y=\frrac{8}{5}x$
Khi $x=12$ thì: $y=\frac{8}{5}x=\frac{8}{5}.12=19,2$

a: Ta có: \(\widehat{BAE}=\widehat{BAC}+\widehat{CAE}=\widehat{BAC}+90^0\)
\(\widehat{CAD}=\widehat{CAB}+\widehat{DAB}=\widehat{BAC}+90^0\)
Do đó: \(\widehat{BAE}=\widehat{DAC}\)
Xét ΔBAE và ΔDAC có
BA=DA
\(\widehat{BAE}=\widehat{DAC}\)
AE=AC
Do đó: ΔBAE=ΔDAC
=>BE=DC
Ta có: ΔBAE=ΔDAC
=>\(\widehat{AEB}=\widehat{ACD}\)
=>\(\widehat{AEK}=\widehat{ACK}\)
=>AECK là tứ giác nội tiếp
=>\(\widehat{CKE}=\widehat{CAE}=90^0\)
=>DC\(\perp\)BE tại K
b: Ta có: ΔKBC vuông tại K
mà KM là đường trung tuyến
nên \(KM=\dfrac{BC}{2}=3\left(cm\right)\)

\(3x=y\)
\(\Rightarrow x=\dfrac{y}{3}\)
\(\Rightarrow\dfrac{x}{4}=\dfrac{y}{12}\) (1)
\(5y=4z\)
\(\Rightarrow\dfrac{y}{4}=\dfrac{z}{5}\)
\(\Rightarrow\dfrac{y}{12}=\dfrac{z}{15}\) (2)
Từ (1) và (2) \(\Rightarrow\dfrac{x}{4}=\dfrac{y}{12}=\dfrac{z}{15}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\dfrac{x}{4}=\dfrac{y}{12}=\dfrac{z}{15}=\dfrac{6x}{24}=\dfrac{7y}{84}=\dfrac{8z}{120}=\dfrac{6x+7y+8z}{24+84+120}=\dfrac{456}{228}=2\)
\(\Rightarrow\left\{{}\begin{matrix}x=2\cdot4=8\\y=2\cdot12=24\\z=2\cdot15=30\end{matrix}\right.\)
Vậy x = 8, y = 24 và z = 30

c: Xét ΔADB và ΔAEC có
AB=AC
\(\widehat{ABD}=\widehat{ACE}\)
BD=CE
Do đó: ΔADB=ΔAEC
=>AD=AC
Xét ΔHDB vuông tại H và ΔKEC vuông tại K có
BD=CE
\(\widehat{HBD}=\widehat{KCE}\)
Do đó: ΔHBD=ΔKCE
=>HD=KE
Ta có: ΔHBD=ΔKCE
=>\(\widehat{HDB}=\widehat{KEC}\)
mà \(\widehat{HDB}=\widehat{IDE}\)(hai góc đối đỉnh)
và \(\widehat{KEC}=\widehat{IED}\)(hai góc đối đỉnh)
nên \(\widehat{IDE}=\widehat{IED}\)
=>IE=ID
ta có: HD+DI=HI
KE+EI=KI
mà HD=KE và DI=EI
nên HI=KI
Ta có: AH+HB=AB
AK+KC=AC
mà HB=KC và AB=AC
nên AH=AK
Xét ΔAHI vuông tại H và ΔAKI vuông tại K có
AI chung
AH=AK
Do đó: ΔAHI=ΔAKI
=>\(\widehat{HAI}=\widehat{KAI}\)
=>AI là phân giác của góc BAC

\(\dfrac{x}{2}=\dfrac{y}{3}\)
=>\(\dfrac{x}{8}=\dfrac{y}{12}\left(1\right)\)
\(\dfrac{y}{4}=\dfrac{z}{5}\)
=>\(\dfrac{y}{12}=\dfrac{z}{15}\left(2\right)\)
Từ (1) và (2) suy ra \(\dfrac{x}{8}=\dfrac{y}{12}=\dfrac{z}{15}\)
mà x-y-z=28
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{8}=\dfrac{y}{12}=\dfrac{z}{15}=\dfrac{x-y-z}{8-12-15}=\dfrac{28}{-19}=-\dfrac{28}{19}\)
=>\(x=-\dfrac{28}{19}\cdot8=-\dfrac{224}{19};z=-\dfrac{28}{19}\cdot12=-\dfrac{336}{19};z=-\dfrac{28}{19}\cdot15=-\dfrac{420}{19}\)
\(\dfrac{x}{2}=\dfrac{y}{3}\Rightarrow\dfrac{x}{8}=\dfrac{y}{12}\left(1\right)\\ \dfrac{y}{4}=\dfrac{z}{5}\Rightarrow\dfrac{y}{12}=\dfrac{z}{15}\left(2\right)\\ \left(1\right),\left(2\right)\Rightarrow\dfrac{x}{8}=\dfrac{y}{12}=\dfrac{z}{15}\)
Áp dụng TC dãy tỉ số bằng nhau :
\(\dfrac{x}{8}=\dfrac{y}{12}=\dfrac{z}{15}=\dfrac{x-y-z}{8-12-15}=\dfrac{28}{-19}\\ \Rightarrow\left\{{}\begin{matrix}x=-\dfrac{224}{19}\\y=-\dfrac{336}{19}\\z=-\dfrac{420}{19}\end{matrix}\right.\)

Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x-1}{2005}=\dfrac{3-y}{2006}=\dfrac{x-1+3-y}{2005+2006}=\dfrac{4009+2}{4011}=1\)
=>\(x-1=2005;3-y=2006\)
=>x=2005+1=2006; y=3-2006=-2003
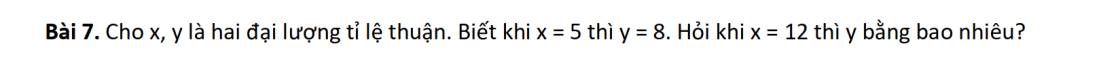



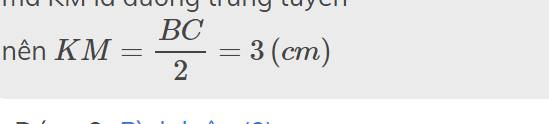
Bài 4:
$P(x)=x^2+5x+6=(x^2+2x)+(3x+6)=x(x+2)+3(x+2)=(x+2)(x+3)$
$P(x)=0$
$\Rightarrow (x+2)(x+3)=0$
$\Rightarrow x+2=0$ hoặc $x+3=0$
$\Rightarrow x=-2$ hoặc $x=-3$
Vậy $x=-2$ và $x=-3$ là hai nghiệm của đa thức.
Bài 5:
a. Để $x=0$ là nghiệm của $P(x)$ thì:
$P(0)=0$
$\Rightarrow 2.0+a-1=0$
$\Rightarrow a-1=0$
$\Rightarrow a=1$
b.
Để $x=1$ là nghiệm của $P(x)$ thì:
$P(1)=0$
$\Rightarrow 2.1+a-1=0$
$\Righrarrow a+1=0$
$\Rightarrow a=-1$