Tìm hai số tự nhiên, biết tổng của chúng là 21 và tổng hai bình phương là 261.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
12 tháng 3 2022
c
Cho tam giác ABCABC vuông tại AA. Nửa đường tròn đường kính ABAB cắt BCBC tại DD. Trên cung ADAD lấy một điểm EE. Nối BEBE và kéo dài cắt ACAC tại FF. Chứng minh CDEFCDEF là tứ giác nội tiếp.
theo gt, ta có: DAB = BCA= 90 - CBA
(Tính chất tổng các góc trong tam giác BCA và tam giác BAD)
Mặt khác DEB = DAB ( Cùng chắn cung DB)
=> DEB= BCA => Đpcm
12 tháng 3 2022
Cho tam giác ABCABC cân tại AA và nội tiếp đường tròn tâm OO, đường kính AIAI. Gọi EE là trung điểm của ABAB, KK là trung điểm của OIOI, HH là trung điểm của EBEB.
a/ Chứng minh HK\perp EBHK⊥EB
b/ Chứng minh tứ giác AEKCAEKC nội tiếp được trong một đường tròn.
a) Ta thấy E, O là trung điểm của AB và AI nên EO là đường trung bình tam giác ABI
\Rightarrow⇒ EO song song với BI.
Ta lại có H, K lần lượt là trung điểm của EB và OI
nên HK là đường trung bình của hình thang EOIB.
=> HK song song với BI (1)
Mặt khác do AI là đường kính nên góc ABI = 90 (2)\widehat{ABI}=90^o
Từ (1) và (2) suy ra HK\perp EBHK vuông góc với EB(đpcm)
b)
Xét tam giác KBE có KH là trung tuyến đồng thời đường cao (CM trước)
nên KBE là tam giác cân tại K.
=> góc BEK = KBE (3)
Do tam giác ABC cân tại A
nên AI là đường trung trực của BC
Mà K thuộc AI nên KB = KC
hay tam giác KBC cân tại K
=> KBC=KCB
và ACB=ABC
.Mặt khác, ta lại có ACB= ACK + KCB và ABC = ABK + KBC
=> ABK=ACK(4)
Từ (3) và (4) suy ra \widehat{BEK}=\widehat{KCA}
.
AEKC là tứ giác nội tiếp.
12 tháng 3 2022
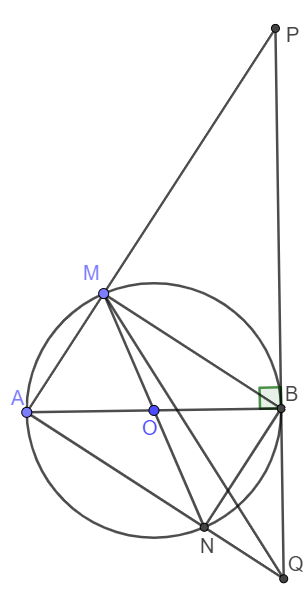
Cho ABAB và MNMN là hai đường kính khác nhau của đường tròn (O)(O). Tiếp tuyến tại BB của (O)(O) cắt các đường thẳng AMAM, ANAN lần lượt tại PP và QQ. Chứng minh:
a) ABMNABMN là hình chữ nhật.
b) Bốn điểm MM, NN, PP, QQ cùng thuộc một đường tròn.
a) Theo gt, ta có :
ABAB và MNMN là hai đường kính khác nhau của đường tròn (O)(O)
=> góc MAN= MBN=AMB=ANB (tính chất góc nội tiếp nhìn nửa đường tròn)
=> AMBN là hình chữ nhật (đpcm)
b) Ta thấy:
MNA= MBA (cùng chắn cung MA)
MBA= 90 - PAB (tính chất tổng 3 góc trong tam giác MBA)
MPB= 90 - PAB (tính chất tổng 3 góc trong tam giác MPB)
=> MNA = MPA => đpcm (vì là tứ giác có góc ngoài tam giác bằng góc đối trong tứ giác)
12 tháng 3 2022
Cho đường tròn tâm OO đường kính MNMN và AA là một điểm trên đường tròn (O)(O), (AA khác MM và AA khác NN). Lấy một điểm II trên đoạn thẳng ONON (II khác OO và II khác NN). Qua II kẻ đường thẳng (d)(d) vuông góc với MNMN. Gọi PP, QQ lần lượt là giao điểm của AMAM, ANAN với đường thẳng (d)(d). Gọi KK là điểm đối xứng của NN qua điểm II. Chứng minh góc PMK = IQN\widehat{PMK}=\widehat{IQN}
và tứ giác MPQKMPQK nội tiếp đường tròn.
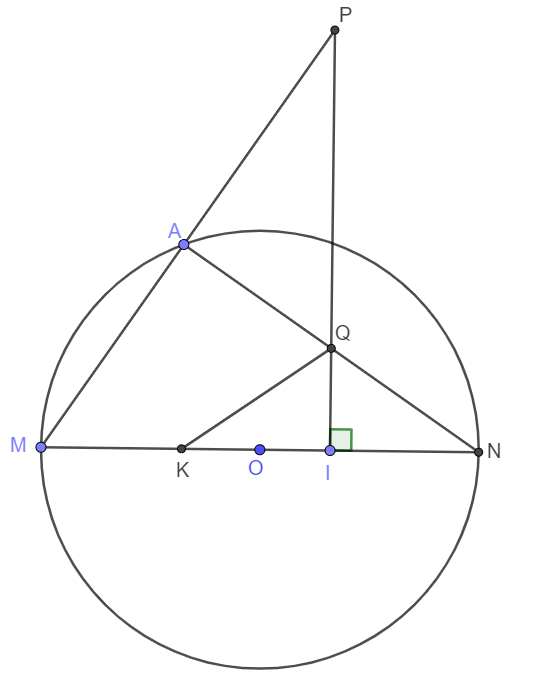
Xét 2 tam giác AMN và IQN có :
góc A= goc QIN= 90 (gt)
=> goc M= IQN= 90 - goc N (đpcm)
Xet 2 tam giác IQK và IQN có:
IQ chung
vì K là điểm đối xứng của NN qua điểm II
=> IK =IN
góc QIK = QIN=90
=> 2 tam giác IQK = IQN (c.g.c)
=> góc IQK=IQN=PQA=PMK
trong đó góc PQK + IQN = 180
=> góc PQK + PMK = 180
=> đpcm