cho mik hỏi là có mẹo nào để nhận biết TỈ LỆ THUẬN và TỈ LỆ NGHỊCH ko mình đọc thuộc định nghĩa nhưng vẫn ko biết cách phân biệt
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét ΔABC và ΔCDA có
\(\widehat{BAC}=\widehat{DCA}\)(hai góc so le trong, BA//CD)
AC chung
\(\widehat{BCA}=\widehat{DAC}\)(hai góc so le trong, AD//BC)
Do đó: ΔABC=ΔCDA
b: Ta có: ΔABC=ΔCDA
=>AB=CD và BC=DA
Xét ΔADB và ΔCBD có
AD=CB
BD chung
AB=CD
Do đó: ΔADB=ΔCBD
c: Xét ΔOAD và ΔOCB có
\(\widehat{OAD}=\widehat{OCB}\)(hai góc so le trong, AD//BC)
AD=BC
\(\widehat{ODA}=\widehat{OBC}\)(hai góc so le trong, AD//BC)
Do đó: ΔOAD=ΔOCB
=>OA=OC và OD=OB
Xét ΔABO và ΔCDO có
AB=CD
OB=OD
OA=OC
Do đó: ΔABO=ΔCDO

a: Xét ΔABM và ΔACM có
AB=AC
BM=CM
AM chung
Do đó: ΔABM=ΔACM
b: Ta có: ΔABM=ΔACM
=>\(\widehat{MAB}=\widehat{MAC}\)
Xét ΔAHM vuông tại H và ΔAKM vuông tại K có
AM chung
\(\widehat{HAM}=\widehat{KAM}\)
Do đó: ΔAHM=ΔAKM
=>AH=KA
Xét ΔAHK có AH=AK
nên ΔAHK cân tại A

Lời giải:
Áp dụng TCDTSBN:
$\frac{1}{x+y+z}=\frac{y+z+1}{x}=\frac{x+z+2}{y}=\frac{x+y-3}{z}=\frac{y+z+1+x+z+2+x+y-3}{x+y+z}=\frac{2(x+y+z)}{x+y+z}=2$
$\Rightarrow x+y+z=\frac{1}{2}$
Có:
$\frac{y+z+1}{x}=\frac{x+z+2}{y}=\frac{x+y-3}{z}=2$
$\Rightarrow \frac{y+z+1}{x}+1=\frac{x+z+2}{y}+1=\frac{x+y-3}{z}+1=3$
$\Rightarrow \frac{x+y+z+1}{x}=\frac{x+y+z+2}{y}=\frac{x+y+z-3}{z}=3$
$\Rightarrow \frac{1,5}{x}=\frac{2,5}{y}=\frac{-2,5}{z}=3$
$\Rightarrow x=0,5; y=\frac{5}{6}; z=\frac{-5}{6}$

a: Xét ΔABF và ΔAEC có
AB=AE
\(\widehat{BAF}=\widehat{EAC}\)(hai góc đối đỉnh)
AF=AC
Do đó: ΔABF=ΔAEC
=>BF=EC
Xét ΔAEF và ΔABC có
AE=AB
\(\widehat{EAF}=\widehat{BAC}\)(hai góc đối đỉnh)
AF=AC
Do đó: ΔAEF=ΔABC
=>\(\widehat{AEF}=\widehat{ABC}\)
mà hai góc này là hai góc ở vị trí so le trong
nên EF//BC
b: Ta có: FM+MB=FB
=>FB=2MF+MF=3MF
mà CE=3CN
và FB=CE
nên MF=CN
Xét ΔAFM và ΔACN có
AF=AC
\(\widehat{AFM}=\widehat{ACN}\)(ΔAFB=ΔACE)
FM=CN
Do đó: ΔAFM=ΔACN
=>\(\widehat{FAM}=\widehat{CAN}\)
mà \(\widehat{FAM}+\widehat{MAC}=180^0\)(hai góc kề bù)
nên \(\widehat{CAN}+\widehat{CAM}=180^0\)
=>M,A,N thẳng hàng

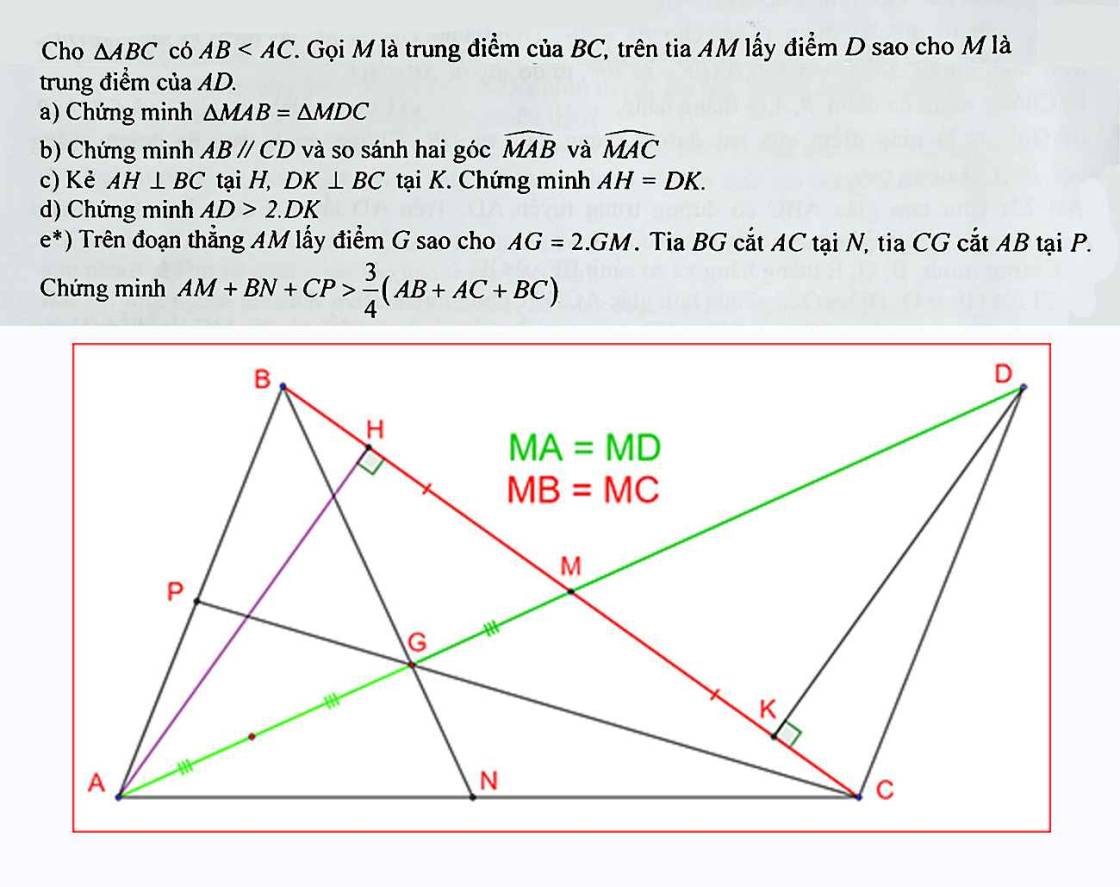
a: Xét ΔMAB và ΔMDC có
MA=MD
\(\widehat{AMB}=\widehat{DMC}\)(hai góc đối đỉnh)
MB=MC
Do đó: ΔMAB=ΔMDC
b: ta có: ΔMAB=ΔMDC
=>\(\widehat{MAB}=\widehat{MDC}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AB//CD
Ta có: ΔMAB=ΔMCD
=>AB=CD
mà AB<AC
nên CD<CA
=>\(\widehat{CAD}< \widehat{CDA}\)
mà \(\widehat{CDA}=\widehat{BAM}\)
nên \(\widehat{CAM}< \widehat{BAM}\)
c: Xét ΔAHM vuông tại H và ΔDKM vuông tại K có
MA=MD
\(\widehat{AMH}=\widehat{DMK}\)(hai góc đối đỉnh)
Do đó: ΔAHM=ΔDKM
=>AH=DK
d: Ta có: AM>AH(ΔAHM vuông tại H)
DM>DK(ΔDKM vuông tại K)
Do đó: AM+DM>AH+DK
=>AD>2DK
e:
Ta có: AG=2GM
mà AG+GM=AM
nên \(AG=\dfrac{2}{3}AM\)
Xét ΔBAC có
AM là đường trung tuyến
\(AG=\dfrac{2}{3}AM\)
Do đó: G là trọng tâm của ΔABC
Xét ΔABC có
G là trọng tâm của ΔABC
BG cắt AC tại N
CG cắt AB tại P
Do đó: N là trung điểm của AC, P là trung điểm của AB
Xét ΔABC có
G là trọng tâm của ΔABC
BN,CP là các đường trung tuyến
Do đó: \(BG=\dfrac{2}{3}BN;CG=\dfrac{2}{3}CP\)
Xét ΔGAB có GA+GB>AB
Xét ΔGAC có GA+GC>AC
Xét ΔGBC có GB+GC>BC
Do đó: \(2\left(GA+GB+GC\right)>AB+AC+BC\)
=>\(GA+GB+GC>\dfrac{AB+AC+BC}{2}\)
=>\(\dfrac{2}{3}\left(AM+BN+CP\right)>\dfrac{AB+AC+BC}{2}\)
=>\(AM+BN+CP>\dfrac{3}{4}\cdot\left(AB+AC+BC\right)\)

\(\dfrac{2}{3}:\left(x-\dfrac{1}{3}\right)^3-9=\dfrac{23}{3}\)
=>\(\dfrac{2}{3}:\left(x-\dfrac{1}{3}\right)^3=\dfrac{23}{3}+9=\dfrac{50}{3}\)
=>\(\left(x-\dfrac{1}{3}\right)^3=\dfrac{2}{3}:\dfrac{50}{3}=\dfrac{1}{25}\)
=>\(x-\dfrac{1}{3}=\dfrac{\sqrt[3]{5}}{5}\)
=>\(x=\dfrac{\sqrt[3]{5}}{5}+\dfrac{1}{3}=\dfrac{3\sqrt[3]{5}+5}{15}\)

Tỉ lệ nghịch là 2 đại lượng đối nghịch nhau, kiểu như cái này tăng thì cái kia giảm (tc thì xét tích tương ứng). - Tỉ lệ thuận là 2 đại lượng cùng tăng và cùng giảm (tc thì xét tỉ số).