-108= bao nhiêu mũ 2?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét ΔDBA vuông tại D và ΔABC vuông tại A có
\(\widehat{DBA}\) chung
Do đó: ΔDBA~ΔABC
b: ΔDBA~ΔABC
=>\(\dfrac{BD}{BA}=\dfrac{BA}{BC}\left(1\right)\)
Xét ΔBAD có BF là phân giác
nên \(\dfrac{BD}{BA}=\dfrac{FD}{FA}\left(2\right)\)
Xét ΔBAC có BE là phân giác
nên \(\dfrac{BA}{BC}=\dfrac{AE}{EC}\left(3\right)\)
Từ (1),(2),(3) suy ra \(\dfrac{FD}{FA}=\dfrac{AE}{EC}\)
=>\(FD\cdot EC=AE\cdot FA\)

a: \(\left(\dfrac{1}{4}+\dfrac{-3}{11}\right)+\left(\dfrac{2}{11}+\dfrac{-8}{11}+\dfrac{3}{4}\right)\)
\(=\dfrac{1}{4}+\dfrac{-3}{11}+\dfrac{2}{11}+\dfrac{-8}{11}+\dfrac{3}{4}\)
\(=\left(\dfrac{1}{4}+\dfrac{3}{4}\right)-\dfrac{9}{11}=1-\dfrac{9}{11}=\dfrac{2}{11}\)
b: \(\left(-1\dfrac{1}{3}+1\dfrac{1}{2}\right)+2\dfrac{1}{2}\)
\(=-1-\dfrac{1}{3}+1+\dfrac{1}{2}+2+\dfrac{1}{2}\)
\(=2+1-\dfrac{1}{3}=3-\dfrac{1}{3}=\dfrac{8}{3}\)
c: \(\left(-2\dfrac{1}{4}\right)+\dfrac{5}{2}:3\dfrac{3}{4}\)
\(=-\dfrac{9}{4}+\dfrac{5}{2}:\dfrac{15}{4}\)
\(=-\dfrac{9}{4}+\dfrac{5}{2}\cdot\dfrac{4}{15}=\dfrac{-9}{4}+\dfrac{2}{3}\)
\(=\dfrac{-27+8}{12}=-\dfrac{19}{12}\)
d: \(\dfrac{5}{8}:0,25-\left(0,6-2\dfrac{1}{4}\right):2\dfrac{1}{5}\)
\(=\dfrac{5}{8}:\dfrac{1}{4}-\left(\dfrac{3}{5}-\dfrac{9}{4}\right):\dfrac{11}{5}\)
\(=\dfrac{5}{2}-\dfrac{12-45}{20}\cdot\dfrac{5}{11}\)
\(=\dfrac{5}{2}-\dfrac{5}{20}\cdot\dfrac{-33}{11}=\dfrac{5}{2}+\dfrac{3}{4}=\dfrac{13}{4}\)
e: \(1\dfrac{1}{2}\cdot1\dfrac{1}{3}\cdot...\cdot1\dfrac{1}{999}\)
\(=\dfrac{3}{2}\cdot\dfrac{4}{3}\cdot...\cdot\dfrac{1000}{999}\)
\(=\dfrac{1000}{2}=500\)
f: \(\left(\dfrac{1}{2}-1\right)\left(\dfrac{1}{3}-1\right)\cdot...\cdot\left(\dfrac{1}{100}-1\right)\)
\(=\dfrac{-1}{2}\cdot\dfrac{-2}{3}\cdot...\cdot\dfrac{-99}{100}=-\dfrac{1}{100}\)

e: Chiều dài hình chữ nhật là: \(\dfrac{4y^2+4y-3}{2x-1}\left(cm\right)\)
f: Chiều rộng của hình hộp là:
\(\dfrac{3x^3+8x^2-45x-40}{\left(x+5\right)\left(x+1\right)}\)
\(=\dfrac{3x^3+8x^2-45x-40}{x^2+6x+5}\)
\(=\dfrac{3x^3+18x^2+15x-10x^2-60x-50+10}{x^2+6x+5}\)
\(=3x-10+\dfrac{10}{x^2+6x+5}\left(cm\right)\)

a: Thể tích của bể nước là:
\(2\cdot1,5\cdot1,2=3,6\left(m^3\right)=3600\left(lít\right)\)
b: thể tích nước đã chảy vào bể là:
4x600=2400(lít)=2,4m3
Chiều cao của mực nước là:
2,4:2:1,5=1,2:1,5=0,8(m)

7: vận tốc của cano lúc xuôi dòng là:
24+3=27(km/h)
1h40p=5/3(giờ)
Độ dài quãng đường là \(27\times\dfrac{5}{3}=45\left(km\right)\)

Độ dài quãng đường AB là:
\(9:\left(\dfrac{1}{2}-\dfrac{1}{5}\right)=9:\dfrac{3}{10}=9\times\dfrac{10}{3}=30\left(km\right)\)

Đây là chuyên đề nâng cao, điểm và đường thẳng. cấu trúc thi chuyên, thi học sinh giỏi các cấp. Hôm nay, Olm.vn sẽ hướng dẫn các em giải các dạng này như sau
a; Không có 3 diểm nào thẳng
Cứ 1 điểm sẽ tạo với 60 - 1 điểm còn lại 60 - 1 đường thẳng.
Với 60 điểm sẽ tạo được số đường thẳng là:
(60 - 1) x 60 (đường thẳng)
Theo cách tính trên mỗi đường thẳng sẽ được tính hai lần.
Vậy thực tế số đường thẳng được tạo từ 60 điểm là:
(60 - 1) x 60 : 2 = 1770 (đường thẳng)
Kết luận: Với 60 điểm trong đó bất cứ 3 điểm nào cũng không thẳng hàng, qua 2 điểm có thể dựng được số đường thẳng là 1770 đường thẳng.
b; Có đúng 7 điểm thẳng hàng:
Số điểm trong đó không có 3 điểm nào thẳng hàng là:
60 - 7 = 53 (điểm)
Xét 53 điểm trong đó không có 3 điểm nào thẳng hàng ta có:
Cứ 1 điểm sẽ tạo với 53 - 1 điểm còn lại 53 - 1 đường thẳng.
Với 57 điểm sẽ tạo được số đường thẳng là:
(53 - 1) x 53 (đường thằng)
Theo cách tính trên mỗi đường thẳng được tính hai lần, vậy thực tế số đường thẳng được tạo là:
(53 - 1) x 53 : 2 = 1378 (đường thẳng)
Qua 7 điểm thẳng hàng ta có 1 đường thẳng d
Với 1 điểm nằm ngoài đường thẳng d ta sẽ tạo được với 7 điểm trên d đường thẳng.
Với 53 điểm nằm ngoài d sẽ tạo được được số đường thẳng là:
7 x 53 = 371 (đường thẳng)
Từ những lập luận trên ta có tất cả số đường thẳng được tạo là:
1378 + 1 + 371 = 1750 (đường thẳng)
Kết luận:...

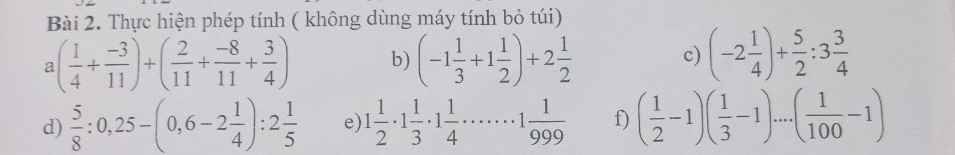



-108 ko thể được số nào mũ 2 được nhé vì âm nhân âm = dương và dương nhân dương= dương