
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


D = 1 + 3² + 3⁴ + ... + 3⁹⁸ + 3¹⁰⁰
⇒ 9D = 3² + 3⁴ + 3⁶ + ... + 3¹⁰⁰ + 3¹⁰²
⇒ 8D = 9D - D
= (3² + 3⁴ + 3⁶ + ... + 3¹⁰⁰ + 3¹⁰²) - (1 + 3² + 3⁴ + ... + 3⁹⁸ + 3¹⁰⁰)
= 3¹⁰² - 1
⇒ D = (3¹⁰² - 1) : 8
\(D=1+3^2+3^4+...+3^{98}+3^{100}\)
=>\(9D=3^2+3^4+...+3^{102}\)
=>\(9D-D=3^2+3^4+...+3^{102}-1-3^2-...-3^{98}-3^{100}\)
=>\(8D=3^{102}-1\)
=>\(D=\dfrac{3^{102}-1}{8}\)

(x . 627 + 37 ) . 215 = ( -2 ) + 37
( x . 627 + 37) . 215 = 35
( x . 627 + 37) = 35 : 215
( x . 627 + 37) = 7/43
x . 627 = 7/43 - 37
x . 627 = - 1584/43
x = -1584/43 : 627
x = -48/817
Vậy x = - 48/817
(x . 627 + 37 ) . 215 = ( -2 ) + 37
( x . 627 + 37) . 215 = 35
( x . 627 + 37) = 35 : 215
( x . 627 + 37) = 7/43
x . 627 = 7/43 - 37
x . 627 = - 1584/43
x = -1584/43 : 627
x = - 48/817
Vậy x = - 48/817

Xét ΔAIB và ΔAIC có
AI chung
IB=IC
AB=AC
Do đó: ΔAIB=ΔAIC
=>\(\widehat{AIB}=\widehat{AIC}\)
mà \(\widehat{AIB}+\widehat{AIC}=180^0\)(hai góc kề bù)
nên \(\widehat{AIB}=\widehat{AIC}=\dfrac{180^0}{2}=90^0\)
=>AI\(\perp\)BC

Gọi độ dài quãng đường AB là x(km)
(ĐK: x>0)
Thời gian đi từ A đến B là \(\dfrac{x}{45}\left(giờ\right)\)
Thời gian đi từ B về A là \(\dfrac{x}{50}\left(giờ\right)\)
Tổng thời gian đi và về là:
1h30p-15p=1h15p=1,25(giờ)
Do đó, ta có phương trình:
\(\dfrac{x}{45}+\dfrac{x}{50}=1,25\)
=>\(\dfrac{10x+9x}{450}=1,25\)
=>19x=1,25*450=562,5
=>\(x=\dfrac{562.5}{19}=\dfrac{1125}{38}\left(nhận\right)\)
Vậy: Độ dài quãng đường AB là 1125/38 km

a: Đặt P(x)=0
=>12-5x=0
=>5x=12
=>x=2,5
b: Đặt Q(y)=0
=>4y-3-5y=0
=>-y-3=0
=>y=-3
c: Đặt E(x)=0
=>\(4x^2-4=0\)
=>\(x^2=1\)
=>\(\left[{}\begin{matrix}x=1\\x=-1\end{matrix}\right.\)
d: Đặt H(x)=0
=>\(x^2+9=0\)
mà \(x^2+9>=9>0\forall x\)
nên \(x\in\varnothing\)

a: \(\dfrac{-2}{9}+\dfrac{8}{15}+1\dfrac{2}{3}-\dfrac{7}{9}+\dfrac{-7}{-15}\)
\(=\left(-\dfrac{2}{9}-\dfrac{7}{9}\right)+\left(\dfrac{8}{15}+\dfrac{7}{15}\right)+\dfrac{5}{3}\)
\(=-1+1+\dfrac{5}{3}=\dfrac{5}{3}\)
b: \(\dfrac{2}{7}\cdot10\dfrac{2}{8}-\dfrac{2}{7}\cdot3\dfrac{1}{4}\)
\(=\dfrac{2}{7}\left(10+\dfrac{1}{4}-3-\dfrac{1}{4}\right)\)
\(=\dfrac{2}{7}\cdot7=2\)
c: \(\dfrac{5}{7}+\dfrac{2}{7}:0,25-0,4\)
\(=\dfrac{5}{7}+\dfrac{2}{7}\cdot4-\dfrac{2}{5}\)
\(=\dfrac{5}{7}+\dfrac{8}{7}-\dfrac{2}{5}=\dfrac{13}{7}-\dfrac{2}{5}=\dfrac{65-14}{35}=\dfrac{51}{35}\)

a: \(A\left(x\right)=4x^2+4x+1\)
bậc là 2
Hạng tử tự do là 1
Hạng tử cao nhất là 4x2
b: A(x)+B(x)=5x2+5x+1
=>\(B\left(x\right)=5x^2+5x+1-A\left(x\right)\)
=>\(B\left(x\right)=5x^2+5x+1-4x^2-4x-1=x^2+x\)
c: \(\dfrac{A\left(x\right)}{2x+1}=\dfrac{4x^2+4x+1}{2x+1}=\dfrac{\left(2x+1\right)^2}{2x+1}=2x+1\)


a: Xét ΔEBC vuông tại E và ΔDCB vuông tại D có
BC chung
\(\widehat{EBC}=\widehat{DCB}\)
Do đó: ΔEBC=ΔDCB
b: Ta có: ΔEBC=ΔDCB
=>\(\widehat{ECB}=\widehat{DBC}\)
=>\(\widehat{HBC}=\widehat{HCB}\)
=>ΔHBC cân tại H
Xét ΔBHC có HB+HC>BC
=>BC<2BH
=>\(BH>\dfrac{BC}{2}\)

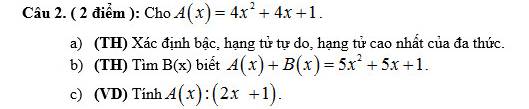

Gọi số vở lớp 7A,7B,7C quyên góp lần lượt là a(quyển),b(quyển),c(quyển)
(ĐIều kiện: \(a,b,c\in Z^+\))
Số vở lớp 7A;7B;7C quyên góp lần lượt tỉ lệ với 2;3;4
=>\(\dfrac{a}{2}=\dfrac{b}{3}=\dfrac{c}{4}\)
Tổng số vở 3 lớp quyên góp là 360 quyển nên a+b+c=360
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{2}=\dfrac{b}{3}=\dfrac{c}{4}=\dfrac{a+b+c}{2+3+4}=\dfrac{360}{9}=40\)
=>\(a=40\cdot2=80;b=40\cdot3=120;c=40\cdot4=160\)
Vậy: số vở lớp 7A,7B,7C quyên góp lần lượt là 80(quyển),120(quyển),160(quyển)