xX(55+45)=987

x X 100=987

x =987:100

x=9,87

\(45\times x+55\times x=987\)

\(x\times\left(45+55\right)=987\)

\(x\times100=987\)

\(x=987:100\)

\(x=9,87\)

Sau hai lần giảm liên tiếp thì được giảm:

\(5\%\times2=10\%\)

Số tiền mà chiếc cặp đó được giảm giá là:

\(300000\div100\times10=30000\left(đồng\right)\)

Người mua phải trả chiếc cặp đó với giá:

\(300000-30000=270000\left(đồng\right)\)

Đáp số: \(270000\left(đồng\right)\)

Sau hai lần giảm liên tiếp thì được giảm:

\(5\%.2=10\%\)

Số tiền chiếc cặp  được giảm giá là:

\(300000:100.100=30000\left(đồng\right)\)

Người mua phải trả chiếc cặp đó với giá:

\(300000-30000=270000\left(đồng\right)\)

                   Đ/S:...

:))

???

???

\(M=\left|x-22\right|+\left|x+12\right|\)

\(M=\left|22-x\right|+\left|x+12\right|\ge\left|22-x+x+12\right|\)

\(M=\left|22-x\right|+\left|x+12\right|\ge34\)

\(M\ge34\)

Dấu "\(=\)" xảy ra khi:

\(\left(22-x\right)\left(x+12\right)\ge0\)

\(TH1:22-x\ge0;x+12\ge0\)

\(\Rightarrow22\ge x\ge-12\)

\(TH2:22-x\le0;x+12\ge0\)

\(\Rightarrow22\le x;x\ge12\left(vô.lý\right)\)

Vậy \(GTNN\) của \(M\) là \(34\) khi \(22\ge x\ge-12\)

\(3x+6xy+2y=7\)

\(\Leftrightarrow3x+6xy+1+2y=8\)

\(\Leftrightarrow3x\left(1+2y\right)+\left(1+2y\right)=8\)

\(\Leftrightarrow\left(3x+1\right)\left(1+2y\right)=8\)

Do \(1+2y\) luôn lẻ với y nguyên nên ta chỉ cần xét các cặp ước của 8 mà \(1+2y\) nhận giá trị lẻ là \(-1;1\)

Vậy \(\left(x;y\right)=\left(-3;-1\right)\) là nghiệm duy nhất

Lời giải:
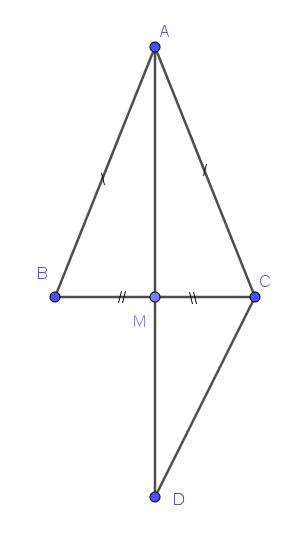
a. Xét tam giác $AMB$ à $AMC$ có:

$AB=AC$ (do tam giác $ABC$ cân tại $A$)

$MB=MC$ (do $M$ là trung điểm $BC$

$AM$ chung

$\Rightarrow \triangle AMB=\triangle AMC$ (c.c.c)

b. 

Từ tam giác bằng nhau phần a

$\Rightarrow \widehat{BAM}=\widehat{CAM}$ 

$\Rightarrow AM$ là phân giác $\widehat{BAC}$

c.

Xét tam giác $ABM$ và $DCM$ có:

$BM=CM$

$AM=DM$ (gt)

$\widehat{AMB}=\widehat{DMC}$ (đối đỉnh) 

$\Rightarrow \triangle ABM=\triangle DCM$ (c.g.c)

$\Rightarrow \widehat{BAM}=\widehat{CDM}$

Mà 2 góc này ở vị trí so le trong nên $AB\parallel CD$

Hình vẽ:

Nãy anh trả lời r nhé

6 km 660 m = 6000 + 660 = 6660 m

= 6660 m