Từ trang 1 đến trang 9 có số trang là :

      ( 9 - 1 ) : 1 + 1 = 9 ( trang )

Từ trang 10 đến trang 99 có số trang là : 

       ( 99 - 10 ) : 1 + 1 = 90 ( trang )

Để trung bình mỗi trang của quyển sách được dùng 2 chữ số để đánh thì trang có 3 chữ số phải bằng số trang có 1 chữ số là 9 .

Quyển sách có số trang là :

        99 + 9 = 108 ( trang )

                    Đáp số : 108 trang.

Từ trang 1 đến trang 9 dùng 1 chữ số

Từ trang 10 đến trang 99 dùng 2 chữ số

Từ trang 100 đến trang 999 dùng 3 chữ số

Vì trung bình mỗi trang phải dùng 2 chữ số nên từ trang 100 phải bù 9 chữ số cho trang 1 đến 9

Vậy số trang của cuốn sách là 108 trang

   1\(\dfrac{1}{3}\) \(\times\) 5\(\dfrac{1}{5}\): 7\(\dfrac{1}{3}\)

=  \(\dfrac{4}{3}\)\(\times\)\(\dfrac{26}{5}\):\(\dfrac{22}{3}\)

=  \(\dfrac{4}{3}\) \(\times\) \(\dfrac{26}{5}\) \(\times\) \(\dfrac{3}{22}\)

= \(\dfrac{52}{55}\)

Tổng số phần bằng nhau:

1+4=5(phần)

Số x bằng:

300:5 x 1= 60

Số y bằng:

300 - 60=240

Đ.số: x=60 và y=240

Tổng hai số là: 300

Tỉ số của hai số là: 1: 4 = \(\dfrac{1}{4}\)

Ta có sơ đồ: 

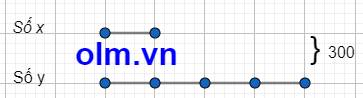
Theo sơ đồ ta có:

Số \(x\) là 300: ( 1 + 4) = 60 

Số y là: 300 - 60 = 240

Đáp số: 60; 240 

1 4/35 + 3 4/7 * 3 1/5 = 39/35 + 25/7 * 16/5 = 39/35 +  80/7 = 39/35 + 400/35 = 439/35

\(1\dfrac{4}{35}+3\dfrac{4}{7}\times3\dfrac{1}{5}=\dfrac{39}{35}+\dfrac{25}{7}\times\dfrac{16}{5}=\dfrac{39}{35}+\dfrac{80}{7}=\dfrac{39}{35}+\dfrac{400}{35}=\dfrac{39+400}{35}=\dfrac{439}{35}\)

ai làm đúng mik tích cho 

đây là đề của chỗ nào? hay bn tự cho?

Vì là số chẵn nên ta có :2 cách chọn chữ số hàng đơn vị (2 hoặc 4) 

  3 cách chọn chữ số hàng chục

  2 cách chọn chữ số hàng trăm

Từ 4 chữ số đó có thể viết đc : (2 x 3 x 2):2= 6 số chẵn có 3 chữ số khác nhau

Số có 3 chữ số có dạng: \(\overline{abc}\)

Trong đó c có: 2 cách chọn

               a có: 3 cách chọn

               b có:  2 cách chọn

          Số các số chẵn có 3 chữ số khác nhau được tạo thành từ các chữ số đã cho là: 

              2 \(\times\) 3 \(\times\) 2 = 12 (số)

Đáp số: 12 số.

quần chúng

quần đảo

não

Hội Liên Hiệp Phụ Nữ

Vậy ban đầu số thứ hai hơn số thứ nhất:

205+104= 309(đơn vị)

Hiệu số phần bằng nhau:

5-2=3(phần)

Số thứ hai ban đầu là:

309:3 x 5= 515

Số thứ nhất ban đầu là:

515 - 309=206

Đáp số: Số thứ nhất 206 và số thứ hai 515