Lời giải:

$\widehat{C}=180^0-(\widehat{A}+\widehat{B})=180^0-(40^0+60^0)=80^0$ (tính chất tổng 3 góc trong tam giác)

Ta thấy: 

$80^0> 60^0> 40^0$

$\Rightarrow \widehat{C}> \widehat{B}> \widehat{A}$

$\Rightarrow AB> AC> BC$ (tính chất cạnh đối diện với góc lớn hơn thì lớn hơn)

a: Xét ΔBEA và ΔBEC có

BE chung

EA=EC

BA=BC

Do đó: ΔBEA=ΔBEC

b: ta có: ΔBEA=ΔBEC

=>\(\widehat{ABE}=\widehat{CBE}\)

=>BE là phân giác của góc ABC

c: Ta có: ΔBEA=ΔBEC

=>\(\widehat{BEA}=\widehat{BEC}\)

mà \(\widehat{BEA}+\widehat{BEC}=180^0\)(hai góc kề bù)

nên \(\widehat{BEA}=\widehat{BEC}=\dfrac{180^0}{2}=90^0\)

=>BE\(\perp\)AC

d: Xét tứ giá ABCK có

AK//BC

AK=BC

Do đó: ABCK là hình bình hành

=>AC cắt BK tại trung điểm của mỗi đường

mà E là trung điểm của AC

nên E là trung điểm của BK

=>B,E,K thẳng hàng

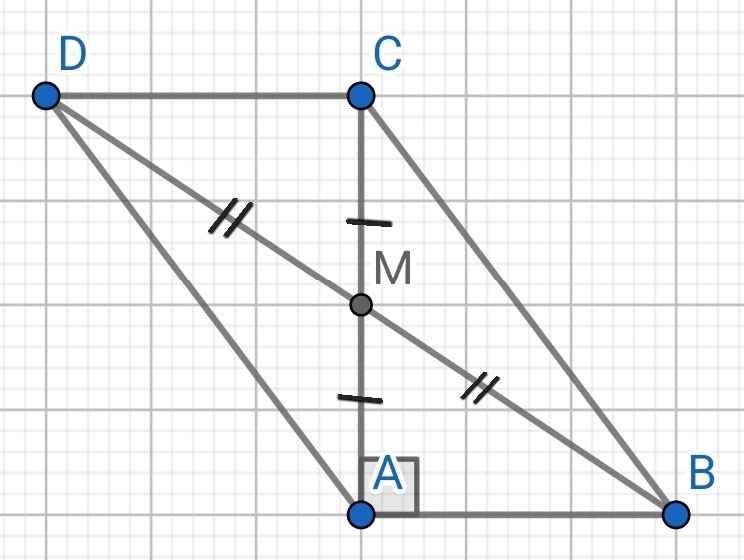
a) Xét ∆ABM và ∆CDM có:

AM = CM (gt)

∠AMB = ∠CMD (đối đỉnh)

MB = MD (gt)

⇒ ∆ABM = ∆CDM (c-g-c)

⇒ AB = CD (hai cạnh tương ứng)

∠BAM = ∠DCM (hai góc tương ứng)

Mà ∠BAM = ∠BAC = 90⁰

⇒ ∠DCM = 90⁰

⇒ CD ⊥ CM

⇒ CD ⊥ AC

b) Xét ∆AMD và ∆CMB có:

AM = CM (gt)

∠AMD = ∠CMB (đối đỉnh)

MD = MB (gt)

⇒ ∆AMD = ∆CMB (c-g-c)

⇒ AD = BC (hai cạnh tương ứng)

∠MAD = ∠MCB (hai góc tương ứng)

Mà ∠MAD và ∠MCB là hai góc so le trong

⇒ AD // BC

c) ∆ABC vuông tại A (gt)

⇒ BC là cạnh huyền nên là cạnh lớn nhất

⇒ BC > AB

Mà AB = CD (cmt)

⇒ BC > CD

∆BCD có:

BC > CD (cmt)

⇒ ∠CDB > ∠CBD

⇒ ∠CDM > ∠CBM

∆ABM = ∆CDM (cmt)

⇒ ∠ABM = ∠CDM (hai góc tương ứng)

Mà ∠CDM > ∠CBM

⇒ ∠ABM > ∠CBM

\(P\left(-1\right)=\left(-1\right)^2+\left(-1\right)^4+\left(-1\right)^6+...+\left(-1\right)^{100}\\ =1+1+1+...+1\\ =50.1=50\)

Giải thích:

Vì dãy: 2, 4, 6, ... , 100

Có : (100 - 2) : 2 + 1 = 50 (số hạng)

x=-1 nên \(x^2=\left(-1\right)^2=1;x^4=\left(-1\right)^4=1;...\left(x^{100}\right)=1\)

Từ 2 đến 100 sẽ có \(\dfrac{100-2}{2}+1=50\left(sốchẵn\right)\)

=>\(P\left(x\right)=1\cdot50=50\)

\(A=\left(\dfrac{1}{3^2}-1\right)\left(\dfrac{1}{4^2}-1\right)\cdot...\cdot\left(\dfrac{1}{10^2}-1\right)\)

\(=\left(\dfrac{1}{3}-1\right)\left(\dfrac{1}{4}-1\right)\cdot...\cdot\left(\dfrac{1}{10}-1\right)\cdot\left(\dfrac{1}{3}+1\right)\left(\dfrac{1}{4}+1\right)\cdot...\cdot\left(\dfrac{1}{10}+1\right)\)

\(=\dfrac{-2}{3}\cdot\dfrac{-3}{4}\cdot...\cdot\dfrac{-9}{10}\cdot\dfrac{4}{3}\cdot\dfrac{5}{4}\cdot...\cdot\dfrac{11}{10}\)

\(=\dfrac{2}{10}\cdot\dfrac{11}{3}=\dfrac{22}{30}=\dfrac{11}{15}\)

a: Xét ΔABD và ΔACE có

AB=AC

\(\widehat{BAD}\) chung

AD=AE

Do đó: ΔABD=ΔACE

b: Ta có: ΔABD=ΔACE

=>\(\widehat{ABD}=\widehat{ACE}\)

Ta có: \(\widehat{ABD}+\widehat{CBD}=\widehat{ABC}\)

\(\widehat{ACE}+\widehat{ECB}=\widehat{ACB}\)

mà \(\widehat{ABD}=\widehat{ACE}\) và \(\widehat{ABC}=\widehat{ACB}\)

nên \(\widehat{CBD}=\widehat{ECB}\)

=>\(\widehat{IBC}=\widehat{ICB}\)

=>ΔIBC cân tại I

c: ta có: AB=AC

=>A nằm trên đường trung trực của BC(1)

Ta có: IB=IC

=>I nằm trên đường trung trực của BC(2)

ta có: MB=MC

=>M nằm trên đường trung trực của BC(3)

Từ (1),(2),(3) suy ra A,I,M thẳng hàng

trả lời đi

a: Ta có: ΔCAB cân tại C

=>\(\widehat{CAB}=\widehat{CBA}\)

mà \(\widehat{CBA}=50^0\)

nên \(\widehat{CAB}=50^0\)

Ta có: ΔCAB cân tại C

=>\(\widehat{ACB}=180^0-2\cdot\widehat{CAB}=80^0\)

Xét ΔCAB có \(\widehat{ACB}>\widehat{CAB}=\widehat{CBA}\)

mà AB,CB,CA lần lượt là cạnh đối diện của các góc ACB,CAB,CBA

nên AB>CB=CA

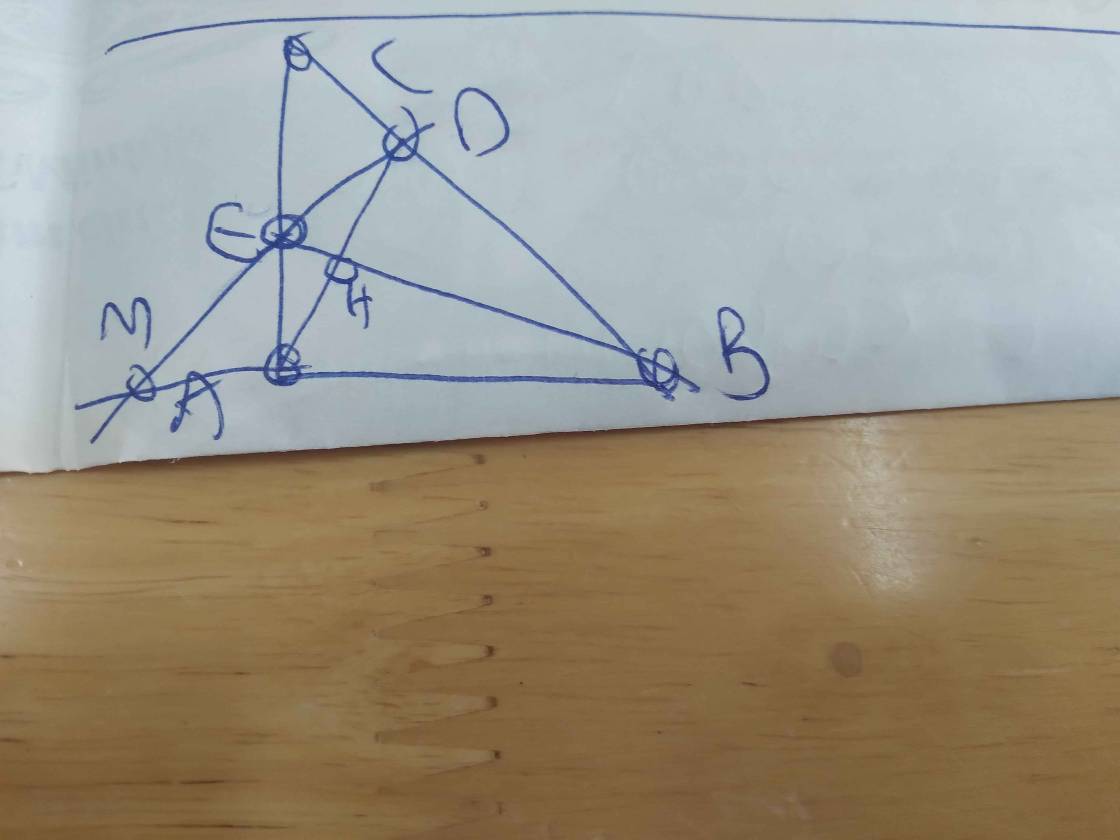
b: Xét ΔCIA vuông tại I và ΔCIB vuông tại I có

CA=CB

CI chung

Do đó: ΔCIA=ΔCIB

=>IA=IB

c: Ta có: ΔCIA=ΔCIB

=>\(\widehat{ACI}=\widehat{BCI}\)

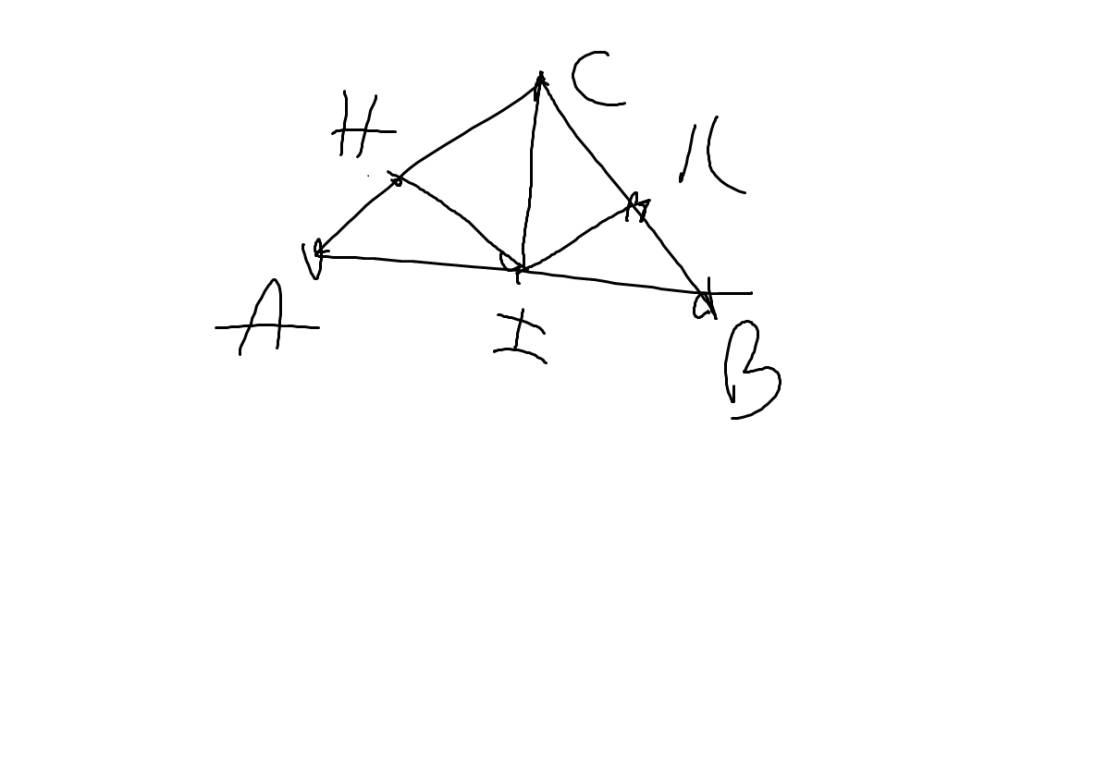
Xét ΔCHI vuông tại H và ΔCKI vuông tại K có

CI chung

\(\widehat{HCI}=\widehat{KCI}\)

Do đó: ΔCHI=ΔCKI

=>IH=IK

d: Ta có: ΔCHI=ΔCKI

=>CH=CK

=>ΔCHK cân tại C