Giúp mình bài này ạ, mai mình thi rồi
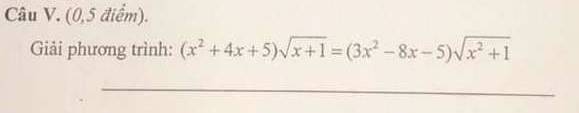
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Có \(\widehat{CAO}=\widehat{CMO}=90^o\) nên \(A,M\) cùng nhìn \(CO\) dưới góc vuông do đó \(C,M,O,A\) cùng thuộc một đường tròn.

Điều kiện đã cho
\(\Leftrightarrow\dfrac{1}{1+a}=\left(1-\dfrac{1}{1+b}\right)+\left(1-\dfrac{1}{1+c}\right)\)
\(\Leftrightarrow\dfrac{1}{1+a}=\dfrac{b}{1+b}+\dfrac{c}{1+c}\)
\(\Leftrightarrow\dfrac{1}{1+a}=\dfrac{b+c+2bc}{bc+b+c+1}\)
\(\Leftrightarrow bc+b+c+1=b+c+2bc+ab+ac+2abc\)
\(\Leftrightarrow2abc+ab+bc+ca=1\)
Mà \(ab+bc+ca\ge3\left(\sqrt[3]{abc}\right)^2\)
\(\Rightarrow2abc+3\left(\sqrt[3]{abc}\right)^2\le1\)
Đặt \(\sqrt[3]{abc}=t\left(t\ge0\right)\), khi đó \(2t^3+3t^2\le1\)
\(\Leftrightarrow\left(t+1\right)^2\left(2t-1\right)\le0\)
Do \(\left(t+1\right)^2\ge0\) nên \(2t-1\le0\) \(\Leftrightarrow t\le\dfrac{1}{2}\) \(\Leftrightarrow abc\le\dfrac{1}{8}\)
Dấu "=" xảy ra khi \(a=b=c=\dfrac{1}{2}\)

<=> 6 căn (x + 5) - 18 = x^ 2 -7x -12v < = > ( 6 căn ( x + 5 ) - 18 ) * ( 6 căn ( x+ 5 ) + 18 ) / ( 6 căn ( x + 5 ) + 18 ) = (x - 4) * ( x -3 ) < = > bạn tính vế chái nần lược rồi thấy thành nhân tử chung là x - 4 => x- 4 =0 => x =4 bạn có thể kiểm cha đáp án nếu thấy sai nhới phản ánh lại nhé
ĐKXĐ :\(\left\{{}\begin{matrix}x+1\ge0\\x^2+1\ge0\end{matrix}\right.\Leftrightarrow x\ge-1\)
Khi đó \((x^2+4x+5)\sqrt{x+1}=(3x^2-8x-5)\sqrt{x^2+1}\)
\(\Leftrightarrow(x^2+1)\sqrt{x+1}+4(x+1)\sqrt{x+1}=3(x^2+1)\sqrt{x^2+1}-8(x+1)\sqrt{x^2+1}\)
Đặt \(\sqrt{x+1}=a;\sqrt{x^2+1}=b(a\ge0;b>0)\)
Phương trình trở thành :
\(4a^3+ab^2=3b^3-8a^2b\)
\(\Leftrightarrow4(a^3+b^3)+b(8a^2+ab-7b^2)=0\)
\(\Leftrightarrow(a+b)(4a^2-4ab+4b^2)+(a+b)(8ab-7b^2)=0\)
\(\Leftrightarrow(a+b)(4a^2+4ab-3b^2)=0\)
\(\Leftrightarrow\left(a+b\right)\left(2a-b\right)\left(2a+3b\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}a+b=0(\text{loại})\\2a-b=0\\2a+3b=0(\text{loại})\end{matrix}\right.\Leftrightarrow2a=b\) (vì \(\left\{{}\begin{matrix}a\ge0\\b>0\end{matrix}\right.\) nên a+b>0 ; 2a +3b > 0)
Trở lại cách đặt ta được
\(2\sqrt{x+1}=\sqrt{x^2+1}\Leftrightarrow x^2-4x-3=0\)
\(\Leftrightarrow x=\pm\sqrt{7}+2\) (loại \(x=-\sqrt{7}+2\))
Vậy x = \(\sqrt{7}+2\) là nghiệm phương trình