 giúp mình vs
giúp mình vs 
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


không được đăng linh tinh trên diễn đàng, nếu đăng bậy nữa chị sẽ báo cáo đó nha!

d) \(\left(2024-x\right)^3+\left(2026-x\right)^3+\left(2x-4050\right)^3=0\) (1)
Đặt: \(\left\{{}\begin{matrix}2024-x=a\\2026-x=b\end{matrix}\right.\Rightarrow2x-4050=-\left(a+b\right)\) (*)
Thay (*) vào pt (1), ta được:
\(a^3+b^3+\left[-\left(a+b\right)\right]^3=0\)
\(\Leftrightarrow\left(a+b\right)^3-3ab\left(a+b\right)-\left(a+b\right)^3=0\)
\(\Leftrightarrow-3ab\left(a+b\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}a=0\\b=0\\a+b=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}2024-x=0\\2026-x=0\\2x-4050=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2024\\x=2026\\x=2025\end{matrix}\right.\)
Vậy \(S=\left\{2024;2025;2026\right\}\).

(y+1)+(y+2)+...+(y+9)=90
=>9y+(1+2+...+9)=90
=>9y+45=90
=>y+5=10
=>y=5

Đây là toán nâng cao chuyên đề chuyển động, cấu trúc thi chuyên, thi học sinh giỏi, thi violympic. Hôm nay Olm.vn sẽ hướng dẫn các em giải chi tiết dạng này như sau:
Giải:
80 m = 0,08 km
Thời gian mà bé Tâm đã chạy từ thềm nhà đến lúc gặp bà ở cổng là:
0,08 : 5 = \(\dfrac{2}{125}\) (giờ)
Khi bé Tâm chạy thì cùng lúc đó con chó Mực cũng chạy. Đến khi bé Tâm dừng vì gặp bà, con chó cũng ngừng chạy nên thời gian con chó chạy bằng thời gian Tâm đã chạy và bằng \(\dfrac{2}{125}\) giờ.
Quãng đường mà con chó Mực đã chạy là:
12 x \(\dfrac{2}{125}\) = 0,192 (km)
Đổi 0,192 km = 192 m
Đáp số: 192 m

a: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
\(\widehat{ABC}\) chung
Do đó: ΔABC~ΔHBA
b: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC=\sqrt{9^2+12^2}=15\left(cm\right)\)
ΔABC~ΔHBA
=>\(\dfrac{AC}{HA}=\dfrac{BC}{BA}\)
=>\(AH=\dfrac{9\cdot12}{15}=\dfrac{108}{15}=7,2\left(cm\right)\)
c: Xét ΔABC có AD là phân giác
nên \(\dfrac{DB}{AB}=\dfrac{DC}{AC}\)
=>\(\dfrac{DB}{9}=\dfrac{DC}{12}\)
=>\(\dfrac{DB}{3}=\dfrac{DC}{4}\)
mà DB+DC=BC=15cm
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{DB}{3}=\dfrac{DC}{4}=\dfrac{DB+DC}{3+4}=\dfrac{15}{7}\)
=>\(DB=\dfrac{45}{7}\left(cm\right);DC=\dfrac{60}{7}\left(cm\right)\)
Để giải bài toán này, chúng ta sẽ sử dụng các tính chất của tam giác vuông và tam giác đồng dạng.
a) Chứng minh tam giác ABC đồng dạng với tam giác HBA; AB^2=BC*HB
Trong tam giác vuông ���ABC, ta có:
- ��=9 cmAB=9cm
- ��=12 cmAC=12cm
Theo định lý Pythagoras, ta có ��=��2−��2=122−92=144−81=63BC=AC2−AB2=122−92=144−81=63.
Từ đó, ta có: ��2=92=81AB2=92=81 ��=63BC=63
Trong tam giác vuông ���ABC, đường cao ��AH là đường trung tuyến của tam giác vuông ���ABH, vì ��AH chia ��BC thành hai phần bằng nhau.
Vì vậy, ta có ��=��/2=63/2HB=BC/2=63/2.
Tam giác ���ABC và ���HBA có góc vuông tại �A và một góc nhọn khác là góc �B. Do đó, theo góc cạnh góc đồng dạng, chúng ta có thể kết luận ���ABC đồng dạng với ���HBA.
Vậy nên, ta có: ����=����/2=2����HBAB=BC/2AB=2BCAB ��2=��×��AB2=BC×HB
b) Tính độ dài cạnh BC và AH
- Độ dài cạnh ��BC: ��=63BC=63 (đã tính ở trên)
- Độ dài đoạn ��AH: ��AH chính là đoạn cao từ �A xuống ��BC, và trong tam giác vuông ���ABC, ��AH là cạnh huyền. Do đó, ��=��=12 cmAH=AC=12cm.
c) Tính độ dài các đoạn thẳng BD và CD
Tia phân giác của góc �A chia ��BC thành hai đoạn thẳng ��BD và ��CD sao cho: ����=����=912=34CDBD=ACAB=129=43
��BD và ��CD cũng chính là độ dài của các phân đoạn ��BC theo tỉ lệ 3:43:4.
Vậy: ��=33+4×��=37×63BD=3+43×BC=73×63 ��=43+4×��=47×63CD=3+44×BC=74×63
Vậy là chúng ta đã giải xong bài toán!

Giá tiền mỗi quyển vở là:
\(120000:15000=8000\) (đồng)
Số tiền Minh mua vở là:
\(120000\times\dfrac{2}{3}=80000\) (đồng)
Minh đã mua số quyển vở là:
\(80000:8000=10\) (quyển)

Buổi sáng bán được: \(48\times\dfrac{2}{3}=32\left(m\right)\)
Buổi chiều bán được: \(48\times\dfrac{1}{6}=8\left(m\right)\)
Tấm vải còn lại:
48-32-8=8(m)
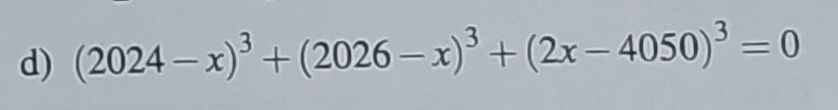


8.
Nửa chu vi vườn rau là:
\(160:2=80\left(m\right)\)
Chiều dài vườn rau là:
\(\left(80+20\right):2=50\left(m\right)\)
Chiều rộng vườn rau là:
\(50-20=30\left(m\right)\)
a.
Diện tích vườn rau là:
\(50\times30=1500\left(m^2\right)\)
b.
Đổi 15kg=0,15 tạ
Số tạ rau thu hoạch được là:
\(1500\times0,15:10=22,5\) (tạ rau)