Quy đồng các phân thức sau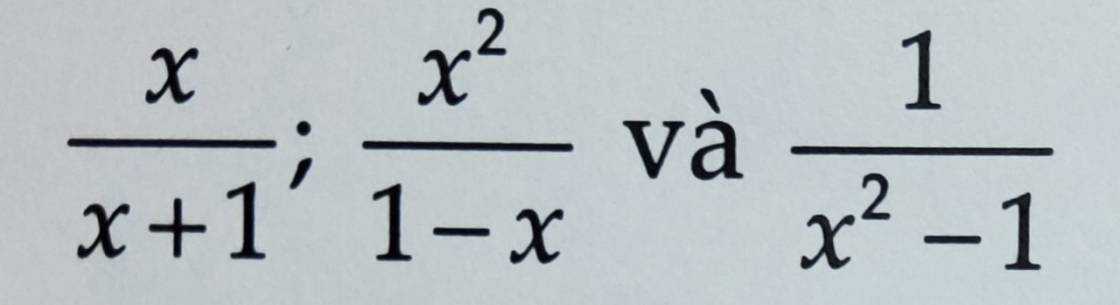
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Cạnh đáy của miếng đất hình tam giác đó là:
\(\left(38+12\right):2=25\left(m\right)\)
Chiều cao của miếng đất hình tam giác đó là:
\(38-25=13\left(m\right)\)
Diện tích miếng đất hình tam giác đó là:
\(\dfrac{25\times13}{2}=162,5\left(m^2\right)\)
Đáp số: \(162,5m^2\)
Độ dài cạnh đáy miếng đất là:
\(\left(38+12\right):2=25\left(m\right)\)
Chiều cao miếng đất là:
\(38-25=13\left(m\right)\)
Diện tích miếng đất là:
\(38\times13:2=247\left(m^2\right)\)

Để tìm số thập phân có 3 chữ số lớn hơn 5 và nhỏ hơn 8, ta có các chữ số có thể sử dụng là 6 và 7.
Có 2 chữ số lớn hơn 5 và nhỏ hơn 8 là 6 và 7. Và mỗi chữ số này có thể điền vào 3 vị trí khác nhau trong số có 3 chữ số.
Vậy số lượng số thập phân có 3 chữ số lớn hơn 5 và nhỏ hơn 8 là 2 * 2 * 2 = 8 số.

A = \(\dfrac{11}{2^3.3^4.5^2}\) = \(\dfrac{11.5}{2^3.3^4.5^3}\) = \(\dfrac{55}{2^3.3^4.5^3}\)
B = \(\dfrac{29}{2^2.3^4.5^3}\) = \(\dfrac{29.2}{2^3.3^4.5^3}\) = \(\dfrac{58}{2^3.3^4.5^3}\)
A < B


A=1+2 mũ 1 +2 mũ 2 + ......+2 mũ 19
suy ra 2A=2 mũ + 2 mũ 2 + ........+ 2 mũ 20
suy ra A = [ 2 mũ 1 + 2 mũ 2 + .......+ 2 mũ 20 ] - [ 1 + 2 mũ 1 + 2 mũ 2 + ....... + 2 mũ 19 ]
suy ra A = 2 mũ 20 -1
suy ra A và B là 2 số tự nhiên liên tiếp
Ko tắt đâu
Ta có:
\(A=2^0+2^1+2^2+2^3+...+2^{19}\)
\(A=1+2+2^2+2^3+...+2^{19}\)
\(2A=2+2^2+2^3+2^4+...+2^{20}\)
\(2A-A=\left(2+2^2+2^3+2^4...+2^{20}\right)-\left(1+2+2^2+2^3+...+2^{19}\right)\)
\(A=2^{20}-1\)
\(\Rightarrow A=2^{20}-1;B=2^{20}\) là hai số liên tiếp.
Vậy...
\(#tutuuu...\)


Lời giải:
$A=\frac{15-3n}{n+2}=\frac{21-3(n+2)}{n+2}=\frac{21}{n+2}-3$
Để $A$ lớn nhất thì $\frac{21}{n+2}$ lớn nhất
Điều này xảy ra khi $n+2>0$ và $n+2$ nhỏ nhất.
Với $n$ nguyên, $n+2>0$ và nhỏ nhất bằng 1
$\Rightarrow n+2=1$
$\Rightarrow n=-1$
------------------------------------
$B=\frac{17-2(2n+1)}{2n+1}=\frac{17}{2n+1}-2$
Để $B$ lớn nhất thì $\frac{17}{2n+1}$ lớn nhất
Điều này xảy ra khi $2n+1>0$ và $2n+1$ nhỏ nhất
Với $n$ nguyên thì $2n+1$ nguyên dương nhỏ nhất bằng 1
$\Rightarrow 2n+1=1$
$\Rightarrow n=0$
\(\dfrac{x}{x+1}=\dfrac{x\left(x-1\right)}{\left(x-1\right)\left(x+1\right)}=\dfrac{x^2-x}{x^2-1}\)
\(\dfrac{x^2}{1-x}=\dfrac{-x^2}{x-1}=\dfrac{-x^2\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}=\dfrac{-x^3-x^2}{x^2-1}\)