Một đơn vị hảo tâm tặng một số máy tính cho ba trường học ở vùng khó khăn để tạo điều kiện giúp đỡ các bạn học sinh thêm cơ họi tiếp xúc với công nghệ thông tin.Biết rằng tổng số máy tính được tặng của trường tỉ lệ với 2;3;4.Tính số máy tính mà đơn vị hảo tâm đã tặng cho mỗi trường.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: \(\dfrac{x}{5}=\dfrac{15}{10}\)
=>\(\dfrac{x}{5}=\dfrac{3}{2}\)
=>\(x=3\cdot\dfrac{5}{2}=7,5\)
b: \(\dfrac{x-5}{3}=\dfrac{x+3}{2}\)
=>3(x+3)=2(x-5)
=>3x+9=2x-10
=>3x-2x=-10-9
=>x=-19
c: \(\dfrac{x}{3}=\dfrac{y}{6}\)
=>\(\dfrac{x}{1}=\dfrac{y}{2}\)
mà x+y=27
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{1}=\dfrac{y}{2}=\dfrac{x+y}{1+2}=\dfrac{27}{3}=9\)
=>\(x=9\cdot1=9;y=9\cdot2=18\)
d: 2x=5y
=>\(\dfrac{x}{5}=\dfrac{y}{2}\)
Đặt \(\dfrac{x}{5}=\dfrac{y}{2}=k\)
=>\(x=5k;y=2k\)
Ta có: xy=10
=>\(5k\cdot2k=10\)
=>\(10k^2=10\)
=>\(k^2=1\)
=>\(\left[{}\begin{matrix}k=1\\k=-1\end{matrix}\right.\)
TH1: k=1
=>\(x=5\cdot1=5;y=2\cdot1=2\)
TH2: k=-1
=>\(x=5\cdot\left(-1\right)=-5;y=2\cdot\left(-1\right)=-2\)

Lời giải:
Gọi $a$ (m) là độ dài đoạn đường.
Theo dự định, đoạn được sẽ được chia thành $5+6+7=18$ phần, 3 tổ sẽ được phân công lần lượt $\frac{5a}{18}, \frac{6a}{18}=\frac{a}{3}, \frac{7a}{18}$ (mét đường)
Thực tế, đoạn đường được chia thành $4+5+6=15$ phần, 3 tổ được phân công lần lượt $\frac{4a}{15}, \frac{5a}{15}=\frac{a}{3}, \frac{6}{15}a=\frac{2}{5}a$ (mét đường)
Như vậy, chỉ có tổ 3 là làm nhiều hơn so với dự kiến.
$\Rightarrow \frac{2}{5}a-\frac{7}{18}a=15$
$\Rightarrow \frac{1}{90}a=15$
$\Rightarrow a=1350$ (m)
Số mét đường chia lại cho:
Tổ 1: $1350.\frac{4}{15}=360$ (m)
Tổ 2: $1350.\frac{1}{3}=450$ (m)
Tổ 3: $1350.\frac{2}{5}=540$ (m)

a: Xét ΔABD vuông tại A và ΔEBD vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)
Do đó: ΔBAD=ΔBED
b: F ở đâu vậy bạn?

a: Xét ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)
Do đó: ΔBAD=ΔBED
b: Sửa đề: DE cắt AB tại F
Ta có: ΔBAD=ΔBED
=>DA=DE
mà DA<DF(ΔDAF vuông tại A)
nên DE<DF

a: Xét ΔBAD có BA=BD
nên ΔBAD cân tại B
=>\(\widehat{BAD}=\widehat{BDA}\)
b: Ta có: \(\widehat{CAD}+\widehat{BAD}=\widehat{BAC}=90^0\)
\(\widehat{HAD}+\widehat{BDA}=90^0\)(ΔHDA vuông tại H)
mà \(\widehat{BAD}=\widehat{BDA}\)
nên \(\widehat{CAD}=\widehat{HAD}\)
Xét ΔAHD vuông tại H và ΔAKD vuông tại K có
AD chung
\(\widehat{HAD}=\widehat{KAD}\)
Do đó: ΔAHD=ΔAKD
=>AH=AK và DH=DK
AH=AK
nên A nằm trên đường trung trực của HK(1)
Ta có: DH=DK
=>D nằm trên đường trung trực của HK(2)
Từ (1) và (2) suy ra AD là đường trung trực của HK

Câu 14:
a: \(\dfrac{a}{b}=\dfrac{b}{d}=\dfrac{e}{f}=\dfrac{a+b+e}{b+d+f}\)
b: \(\dfrac{x}{4}=\dfrac{y}{7}\)
mà x+y=55
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{4}=\dfrac{y}{7}=\dfrac{x+y}{4+7}=\dfrac{55}{11}=5\)
=>\(x=5\cdot4=20;y=5\cdot7=35\)
Câu 15:
a: hệ số tỉ lệ là:
\(k=x\cdot y=4\cdot\left(-8\right)=-32\)
b: xy=-32
=>\(x=-\dfrac{32}{y}\)
Khi y=2 thì \(x=-\dfrac{32}{2}=-16\)
Câu 13:
a: \(7:21=\dfrac{1}{4}:\dfrac{3}{4}\)
\(\dfrac{1}{5}:\dfrac{1}{2}=1:2,5\)
b: \(\dfrac{5}{3}=\dfrac{x}{9}\)
=>\(x=5\cdot\dfrac{9}{3}\)
=>\(x=5\cdot3=15\)

Sửa đề: MA=MK
a: Xét ΔMBK và ΔMCA có
MB=MC
\(\widehat{BMK}=\widehat{CMA}\)(hai góc đối đỉnh)
MK=MA
Do đó: ΔMBK=ΔMCA
=>BK=CA
mà AB=AC
nên BK=BA
=>ΔBAK cân tại B
b: Ta có: ΔMBK=ΔMCA
=>\(\widehat{MBK}=\widehat{MCA}\)
mà hai góc này là hai góc ở vị trí so le trong
nên BK//AC
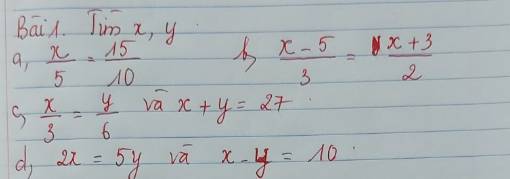



Đề thiếu dữ liệu về tổng số máy tính mà 3 trường được nhận nhé em!